Enunciado
Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 10.Problemas - Ex. 105
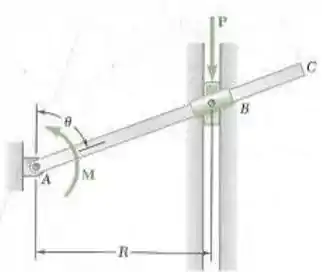
O colar B pode deslizar ao longo da barra AC e é fixado por um pino a um bloco que pode deslizar na fenda vertical como mostrado na figura. Deduza uma expressão da intensidade do binário M, necessário para manter o equilíbrio.
Passo 1
Questão bem simples galera, vamos lá! Primeiro temos que definir alguns parâmetros para usarmos no trabalho virtual! Primeiro, vamos imaginar o triangulo formado pela base, (distancia da origem até a peça) e a altura da base até a peça ():
Passo 2
Agora temos que aplicar o conceito do trabalho virtual para achar o momento para equilíbrio do sistema!
Logo, temos que:
Resposta
Exercícios de Livros Relacionados
33- Uma plataforma automática de carga, projetada para a traseira de um caminhão, está mostrada na figura. A posição da plataforma é controlada pelo cilindro hidráulico, que aplica força em C . As con
68- A figura mostra a vista lateral de uma claraboia uniforme de massa m e com centro de massa na metade da distância entre A e O . A clarabóia é contrabalançada pela ação da mola, que tem uma rigidez
73- Os roletes nas extremidades da barra uniforme A B , de 10k g , se movem livremente nas guias horizontal e vertical, como mostrado. Determine a posição de equilíbrio θ para a barra sob a ação de um
71- O painel retangular uniforme de massa m e centro de massa em G é guiado por roletes- o par superior na guia horizontal e o par inferior na guia vertical. Determine a força P , aplicada a extremida
72- O disco uniforme de alumínio com raio R e massa m rola sem deslizar sobre a superfície circular fixa de raio 2 R . Um cilindro de chumbo também de massa m está preso ao disco e seu centro está loc