Enunciado
Mecânica e Resistência dos Materiais - Dinamica Classica de Particulas e Sistemas - Marion- Ed: 5º - Capítulo 2.Problemas - Ex. 36
Um canhão se localiza sobre uma elevação de altura h sobre o vale de um rio. Se a velocidade de disparo na boca do canhão é v0, determine a expressão para o alcance em função do ângulo de elevação da arma. Resolva numericamente para o alcance máximo no vale para uma determinada altura h e v0.
Passo 1
E aí pessoal, belezinha? Vamos trabalhar agora em algumas questões de mecânica Newtoniana.
Para responder ao questionamento do enunciado, é interessante termos um diagrama da problemática apresentada:
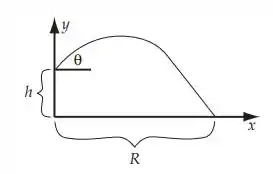
Onde R é o alcance (Range).
Usando a origem como ponto inicial do movimento, temos que as equações para o movimento x e y são:
Chamando de o instante em que o projétil cai no fundo do vale. A equação y dá então:
Uando a solução para uma equação quadrática (Bháskara), teremos que:
Reescrevendo teremos:
Denominando 2gh/v02 de x2, teremos:
Substituindo em t na equação de x, usando o sinal de soma, teremos:
Passo 2
Para maximizarmos o alcance R, devemos fazer:
Embora possa dar x = x(θ), a equação acima não pode ser resolvida para dar θ = θ(x) em termos das funções elementares. O θ ótimo para um dado x é plotado a seguir, juntamente com seu respectivo intervalo em unidades de v02/g. Observe que se x = 0, entre outras coisas corresponde a h = 0, e dá o resultado familiar θ = 45° e R = v02/g.
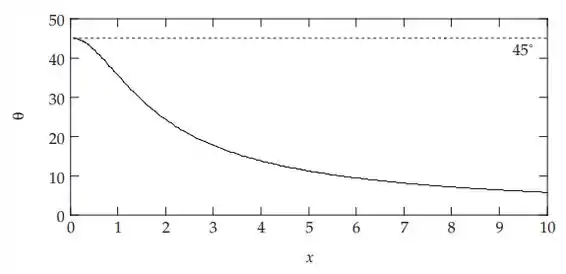
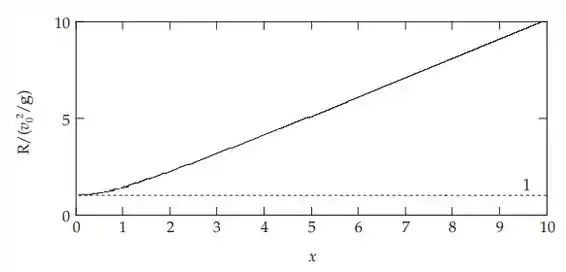
Resposta
Ver passo a passo.