Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 2.4 - Ex. 81

Um fuzil de artilharia de longo alcance em A está apontado em um ângulo de 45 ° com a horizontal, e seu cartucho é somente capaz de transpor o pico de montanha no topo de sua trajetória. Determine o módulo u da velocidade de saída, a altura H da montanha acima do nível do mar, e o alcance R até o mar.

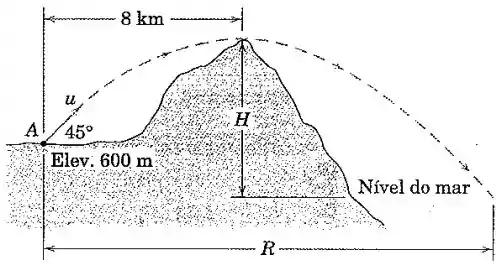
Passo 1

Se a gente equacionar o movimento horizontal, teremos:

x = v x t = u cos ⁡ 45 ° t

Para t = t s , que é o tempo de subida até a altura máxima (o pico da montanha), teremos x = 8   k m = 8000   m :

8000 = u cos ⁡ 45 °   t s

t s = 8000 u cos ⁡ 45 °

Equacionando também o movimento vertical, encontramos:

v y = v 0 y - g t = u   s e n   45 ° - g t

Para t = t s , teremos velocidade v y nula, certo?

0 = u   s e n   45 ° - g 8000 u cos ⁡ 45 °

0 = u 2 2   s e n   45 ° cos ⁡ 45 ° - 2 g 8000

u 2 = 16000 g s e n   90 °

u = 16000   .   9,8

u = 396   m / s

Passo 2

Show! Para encontrar a altura H , basta jogar os dados que temos na fórmula:

y = y 0 + v 0 y t - 1 2 g t 2 = 600 + u   s e n   45 °   t - 1 2 g t 2

Então, vamos ter y = H e t = t s :

H = 600 + u   s e n   45 ° 8000 u cos ⁡ 45 ° - 1 2 g 64 000 000 u 2 cos 2 ⁡ 45 °

H = 600 + 8000   t g   45 ° - 32000000 g u 2 cos 2 ⁡ 45 °

Finalmente, se substituirmos u = 396   m / s e g = 9,8   m / s 2 , encontraremos:

H = 4600   m

Passo 3

Para calcular R , perceba que:

R = u cos ⁡ 45 ° t m = 280 t m

onde t m é o tempo para chegar até o mar.

Para calcularmos t m , vamos usar duas equações do movimento vertical:

v m 2 = v 0 y 2 - 2 g y m - y 0 = u 2   s e n 2   45 ° - 2 g 0 - 600 = 90160   m 2 / s 2

v m = ± 110   m / s

v m = - 300   m / s

Acima o sinal negativo da velocidade foi adotado porque ele cai no mar com velocidade para baixo.

A outra equação vai ser:

v m = v 0 y - g t m = 280 - 9,8 t m

Mas, da primeira, obtemos o valor de v m e o substituímos aqui:

- 300 = 280 - 9,8 t m

t m = 59,2   s

Ou seja,

R = 280 t m = 280   .   59,2 = 16580   m

R = 16,58   k m

Resposta

u = 396   m / s

H = 4600   m

R = 16,58   k m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um projétil é disparado da plataforma em B. O atirador realiza o disparo da sua arma do ponto A a um ângulo de 30°. Determine a velocidade escalar da bala na boca da arma se ela atinge o projétil em C
Determine a velocidade horizontal v A de uma bola de tênis em A de maneira que ela passe raspando a rede em B. Encontre também a distância s medida a partir das redes onde a bola atinge o solo.
Um bombeiro quer direcionar o fluxo de água da sua mangueira para o fogo em B. Determine dois ângulos possíveis θ 1 e θ 2 nos quais isso pode ser feito. A água sai da mangueira a v A = 24m / s .
Um garoto em A tenta jogar uma bola sobre o telhado de um celeiro com uma velocidade escalar inicial de v A = 15m / s . Determine o ângulo θ A no qual a bola deve ser jogada de maneira que ela alcance
Observou-se que o esquiador deixa a rampa A formando um ângulo θ A = 25 ° com a horizontal. Se ele atinge o solo em B, determine sua velocidade escalar inicial v A e o tempo de voo t A B .