Enunciado
Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 14.Problemas - Ex. 4
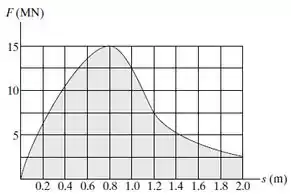
Quando o projétil de 7 kg é disparado de um cano de canhão que tem um comprimento de 2 m, a força explosiva sobre o projétil, enquanto ele está no cano, varia da maneira mostrada. Determine a velocidade aproximada do projétil na boca do canhão no instante que ele deixa o cano. Despreze os efeitos do atrito dentro do cano e suponha que ele seja horizontal.
Passo 1
O enunciado nos dá as seguintes informações:
Massa do projétil: ;
Comprimento do cano: ;
Cano horizontal.
Devemos determinar a velocidade aproximada do projétil na boca do canhão no instante que ele deixa o cano, ou seja, no momento em que o projétil percorre .
Aqui, podemos pensar como dois momentos. No momento (1), antes do disparo, temos que
No momento (2), no instante que o projétil deixa o cano, temos que
Passo 2
Sabemos que o trabalho é igual a área sob o gráfico Força-Deslocamento. Analisando o gráfico, vemos que cada quadrado possui área igual a
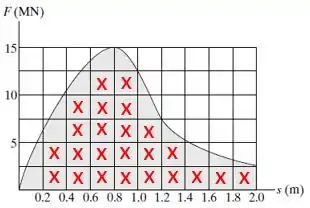
Além disso, vemos que existem 24 quadrados totalmente preenchidos (marcados com um X) e, aproximadamente, 7 quadrados e meio preenchidos ao somar as partes restantantes. Isso resulta em um total de aproximadamente 31,5 quadrados.
A área ocupada por estes quadrado é igual a
Passo 3
Aplicando o Princípio de Trabalho e Energia, temos que
Onde
Substituindo esses valores na equação principal, obtemos