Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 20.Problemas - Ex. 13

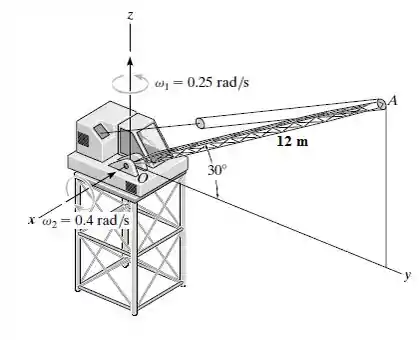
No instante mostrado, o guindaste da torre gira em torno do eixo z com uma velocidade angular ω 1 = 0,25   r a d / s , a qual está aumentando a 0,6   r a d / s ² . A lança do guindaste AO gira para baixo com uma velocidade angular ω 2 = 0,4   r a d / s , a qual está aumentando a 0,8   r a d / s ² .Determine a velocidade e a aceleração do ponto A localizado na extremidade da lança nesse instante.

Passo 1

Definir os vetores de velocidade:

ω s =   ω 1 + ω 2 = 0,25 k - 0,4 i   r a d / s

ω 12 =   - 0,8 i + 0,6 k   r a d / s

Ω = 0.25   k   r a d / s

Passo 2

Encontrando a aceleração angular do guindaste.

α =   ω 12 +   Ω   x   ω s

Substituindo:

α = - 0,8 i + 0.6 k +   0.25 k x   ( - 0,4 i + 0,25   k )

α = - 0.8 i - 0.1 j + 0.6 k r a d / s ²

Passo 3

Encontrar V a :

r a = 12 c o s 30 ° j + 12   s e n 30 ° k =   10,4 j + 6 k

V a = ω s   x   r a = 0,25 j - 0,4 i x   10,4 j + 6 k

V a = - 2,6 i + 2.4 j - 4,16 k m / s

E agora encontrar   a A .

  a A =   α   x   r a +   ω s   x   V a

  a A = - 0.8 i - 0.1 j + 0.6 k   x 10,4 j + 6 k + - 0,4 i + 0,25 k   x   ( - 2,6 i + 2.4 j - 4,16 k )    

  a A = - 7.4 i + 2.5 j - 9,3 k m / s ²

Resposta

Assim a velocidade no ponto A é de - 2,6 i + 2.4 j - 4,16 k m / s e sua aceleração de - 7.4 i + 2 . 5 j - 9,3 k m / s ² .

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

No instante mostrado, o helicóptero está se deslocando para cima com uma velocidade v H = 1,2m / s e tem uma aceleração a H = 0,6m / s 2 . No mesmo instante, a fuselagem H , não o rotor horizontal, gi
No instante mostrado, a estrutura da escavadeira se desloca para frente na direção y com uma velocidade de 2m / s e uma aceleração de 1m / s 2 , enquanto a cabine gira em torno do eixo z com uma veloc
No instante quando θ = 90 ° , o corpo do satélite se desloca na direção x com uma velocidade v O = 500 im / s e aceleração a o = 50 i m / s 2 . Simultaneamente, o corpo também gira com uma velocidade
O cone rola em um círculo e gira em torno do eixo z a uma taxa constante ω z = 8r a d / s . Determine a velocidade e a aceleração angular do cone se ela rola sem deslizar. Além disso, qual é a velocid
No instante quando θ = 90 ° , o corpo do satélite está girando com uma velocidade angular ω 1 = 15r a d / s e aceleração angular ω ˙ 1 = 3r a d / s 2 . Simultaneamente, os painéis solares giram com um