Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 12.Problemas - Ex. 99

Se uma bola de futebol americano é chutada a um ângulo de 45   ° , determine sua velocidade escalar inicial mínima v A de maneira que ela passe sobre o poste do gol em C. A que distância s do poste do gol a bola de futebol vai atingir o solo?

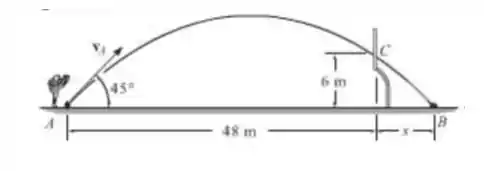
Passo 1

Temos um problema de lançamento oblíquo! A bola possuirá componentes x e y da velocidade. Na direção y , temos a ação da gravidade. É por sua causa que a bola possui uma trajetória arqueada, subindo e posteriormente descendo. Já na direção do eixo x ela possui velocidade constante.

Precisamos determinar inicialmente a mínima velocidade para que a bola passe por cima do gol. Para isto, ela tem que percorrer uma distância x = 48   m ao mesmo tempo que ela sobe, desce e possui uma altura y = 6   m . Esta é a chave da questão. Obter uma relação de tempo e velocidade utilizando as equações do eixo x e depois resolver as do eixo y .

Descoberto esta velocidade, vamos voltar para as equações e descobrir qual o tempo necessário para que y = 0 . Com este tempo, consequentemente teremos a distância x associada. Logo, teremos o valor de s, visto que x = 48 + s ! Vamos as contas então!!!

Passo 2

Vamos começar por obter uma relação de t e v A . Analisando a cinemática na direção do eixo x , temos:

s = s 0 + v x t

48 = 0 + v A cos ⁡ 45 ° t

t = 48 v A cos ⁡ 45 °

t = 48 2 v A

Conseguimos uma relação entre o tempo t e a velocidade v A .

Passo 3

Agora, vamos analisar na direção y . Desta forma, temos:

s = s 0 + v y t + a t 2 2

6 = 0 + v A ⋅ sen ⁡ 45 ° ⋅ t - g t 2 2

6 = v A ⋅ 48 v A - 4,905 ⋅ 4608 v A 2

42 v A 2 = 4,905 ⋅ 4608

v A = 23,2   m / s

Passo 4

Vamos determinar a distância s. Para isto, vamos começar determinando o valor de t para que y = 0 , isto é, a bola suba e desça, retornando a origem do eixo y . Desta forma,

0 = 23,2 ⋅ sen ⁡ 45 ° ⋅ t - g t 2 2

4,905 t 2 - 16,4 t = 0

Resolvendo esta equação, como t ≠ 0 , temos t = 3,34 s . Substituindo este valor na equação da posição da bola na direção x, temos:

x = 23,2 ⋅ cos ⁡ 45 ° ⋅ 3,34

x = 54,9   m

Portanto, a distância s é s = 54,9 - 48 = 6,9   m .

Resposta

v A = 23,2   m / s

s = 6,9   m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma aeronave a jato faz um desvio ascendente em uma curva vertical como apresentado. Quando passa a posição onde θ = 30 ° , sua velocidade é de 1000k m / h e está diminuindo na taxa de 15k m / h por s
Para um determinado intervalo de movimento, o pino P é forçado a se deslocar na ranhura fixa parabólica pela guia vertical ranhurada, que se desloca na direção x na taxa constante de 20m m / s . Todas
No instante representado, suponha que a partícula P , que se move em uma trajetória curva, está a 80m do pólo O e tem a velocidade v e a aceleração a conforme indicado. Determine os valores instantâne
Um foguete lançado verticalmente para cima a partir do pólo norte alcança uma velocidade de 27000k m / h em uma altitude de 350k m quando se esgota o seu combustível. Calcule a altura vertical adicion
Um objeto que é liberado a partir do repouso do topo A de uma torre de altura h parecerá não cair em linha reta devido ao efeito da rotação da Terra. Pode ser demonstrado que o objeto tem uma aceleraç