Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 2.6 - Ex. 168

2/168) Uma cápsula P de fogos de artifício lançada em uma trajetóra vertical tem uma aceleração y dada por a y = - g - k v 2 , onde o último termo é devido ao arrasto aerodinâmico . Se a velocidade da cápsula é de 15 m / s no instante apresentado , determine os valores correspondentes de r , r ' , r " , θ , θ ' e θ " . O parâmetro de arrasto k tem um valor constante de 0,01   m - 1 .

Passo 1

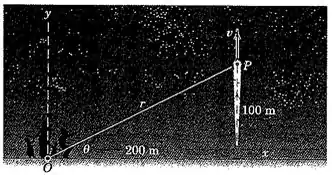
Então galera, a primeira coisa que devemos fazer é achar a distância entre a cápsula P de fogos de artifício e os observadores no instante apresentado através da relação :

r = 200 2 + 100 2 = 224   m

Além disso nós somos capazes de determinar o ângulo θ observado entre o chão e o a reta , que liga o ponto onde estão os observadores e a cápsula , através da fórmula :

θ = tan - 1 ⁡ 100 200 = 26 , 6 °

Passo 2

Agora para acharmos r ' e θ ' usaremos as fórmulas que aprendemos na seção 6 do capítulo 2 .

Temos que :

v r = r ' = v sen ⁡ θ = 15 sen ⁡ 26,6 ° = 6,71 m / s  

Além disso , sabemos que :

v θ = r θ '

15 cos ⁡ 26,6 ° = 224 θ '

θ ' = 0,06   r a d / s

Passo 3

De forma análoga ao item anterior , usaremos as equações obtidas nesta seção do livro , mas desta vez determinaremos r " e θ " . Temos que :

a = - g - k v 2 = - 9,81 - 0,01 15 2 = - 12,06   m / s 2

a r = r " - r θ ' 2

12,06 sen ⁡ 26,6 ° = r " - 224 0,06 2      

r " = - 4,59 m / s 2

E para calcularmos θ " usaremos que :

a θ = r θ " + 2 r ' θ '

- 12,06 cos ⁡ 26,6 ° = 224 θ " + 2 ( 6,71 ) ( 0,06 )

θ " = - 0,0518   r a d / s 2    

Resposta

r = 224   m

θ = 26,6 °

r ' = 6,71 m / s  

θ ' = 0,06   r a d / s

r " = - 4,59 m / s 2

θ " = - 0,0518   r a d / s 2    

De boa galera? Bora fazer mais exercícios então!

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

2/150) Um projétil é lançado a partir do ponto Acom as condições iniciais mostradas . Co m as definições convencionais das coordenadas r e θ em relação ao sistema de coordenadas O x y , determine r ,
2/166) O robô de pinstura é programada para pintar uma linha de produção de superfícies curvas A( vista da borda ) . Ocomprimento do braço telescópico é controlado de acordo com b = 0,3 sen ⁡ π t 2 ,
2/164) O pequeno bloco P parte do repouso no instante t = 0 no ponto A e sobe o plano inclinado com aceleração constante a . Determine r ' como uma função do tempo .
2/155) O cursor P pode ser deslocado para dentro por meio da corda S enquanto a barra AO gira em torno do pivôO . A posição angular da barra é dada por θ = 0,4 + 0,12 t + 0,06 t 3 , onde θ é em radian
2/158) Num determinado instante , uma partícula tem as seguintes componentes de posição , velocidade , e aceleração em relação a um sistema fixo de coordenadas x - y : x = 4 m , y = 2 m , x ' = 2 3m /