Enunciado
Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 12.Problemas de Revisão - Ex. 129
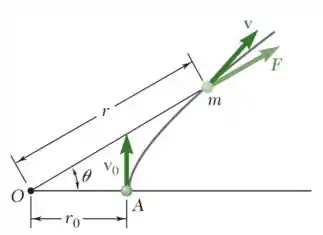
Uma partícula de massa m é lançada do ponto A com uma velocidade inicial v0 perpendicular à linha OA e se move sob a ação da força central F dirigida para fora do centro de força O. Sabendo que a partícula segue uma trajetória definida pela equação r=r0/cos e usando a Eq. (12.27), expresse os componentes radiais e transversais da velocidade v da partícula em função do ângulo .
Passo 1
O enunciado pede que a gente expresse os componentes radiais e transversais da velocidade v da partícula em função do ângulo
Nós temos
Então
Agora
Para que em t=0,
Passo 2
Da Eq. (12.27):
Então
Agora
Ou
e
Resposta
Exercícios de Livros Relacionados
O êmbolo de 5k g acionado por molas é projetado para oscilar na direção vertical sob a ação das duas molas, cada umas das quais possui uma rigidez k =1050N / m e está sem deformação quando x =0 . Se o
O embolo de 5 kg acionado O bloco quadrado homogêneo de massa m é liberado a partir do repouso com θ quase nulo e gira no ponto médio de sua base em torno da quina fixa em O . Determine e represente g
A barra esbelta de 30 kg tem uma velocidade angular inicial de ω=4 rad/s na posição vertical, onde a mola está sem deformação. Determine a velocidade angular mínima de ωmin alcançada pela barra e o ân
A viga uniforme AB de 100kg está perdurada inicialmente em repouso θ=00 quando a força constante P=300 N é aplicada ao cabo. Determine (a) a velocidade angular máxima atingida pela viga com o ângulo θ
Para um trem viaja a 160 km/h por uma curvatura horizontal com raio de 1,9 km, calcule o Ângulo de elevação β do trilho de modo que os passageiros sintam apenas uma força normal nos seus assentos e os