Enunciado
Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 12.Problemas de Revisão - Ex. 131
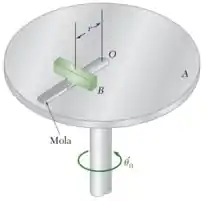
O disco A gira em um plano horizontal em torno de um eixo vertical a uma taxa constante. O cursor B tem uma massa de 230 g e se movimenta em uma fenda sem atrito aberta no disco. O cursor é preso a uma mola de constante k, que não está deformada quando r=0. Sabendo que o cursor é liberado sem velocidade radial na posição r=380 mm, determine a posição do cursor e da força horizontal exercida sobre ele pelo disco em t=0,1s para (a) k=33 N/m, (b) k=48 N/m.
Passo 1
Deixe
Então
ou
ou
ou
Então
Finalmente, para t=0.1s:
Passo 2
Eq. (2)
ou
Resposta
Exercícios de Livros Relacionados
A viga I de aço deve ser transportada pelo carrinho suspenso ao qual está articulada em 0. Se o carrinho parte do repouso com θ ˙ = θ = 0 e recebe uma aceleração horizontal constante α = 2m/s², encont
Determine a massa da Terra sabendo que o raio médio da órbita da Lua em torno da Terra é de 382.250 km e que a Lua precisa de 27,32 dias para completar uma volta inteira em torno da Terra.
Um satélite é colocado em uma órbita circular em torno do planeta Saturno a uma altitude de 2100 milhas. O satélite descreve sua órbita com uma velocidade de 54,7x10³ mi / h. Sabendo que o raio da órb
Os períodos (ver Problema 12.83) das luas do planeta Urano, Julieta e Titânia, foram observados como sendo de 0,4931 dias e 8,706 dias, respectivamente. Sabendo que o raio da órbita de Julieta é 64.36
Um veículo espacial está em uma órbita circular de 2.200 km de raio ao redor da Lua. Para ser transferido para uma órbita menor, de 2.080 km de raio, o veículo é posto primeiro em uma trajetória elípt