Enunciado
Mecânica e Resistência dos Materiais - J. L. Meriam - Estática - Mecânica para Engenharia- Ed: 7º - Capítulo 4.Problemas - Ex. 117
Os projetistas de mecanismos de lâmpadas, como o mostrado na figura, geralmente contam com a fricção das juntas para ajudar a manter o equilíbrio estático. Para o presente problema, suponha que exista atrito suficiente no ponto C para evitar a rotação lá, mas ignore o atrito em todas as outras juntas. Se a massa do suporte da lâmpada for 0,6 kg com centro de massa em G, determine a força da mola FS necessária para o equilíbrio na posição mostrada.
Passo 1
Primeiro, vamos isolar e desenhar o diagrama de corpo livre da luminária de 0,6 kg e membro CG, com as forças dos membros BC e CD atuando nele
Observe que há um par de forças de atrito agindo na junta C impedindo que o acessório gire
O peso da lâmpada é:
O ângulo que os membros BC e CD fazem com a horizontal é:
Passo 2
Ao igualar a soma das forças na direção x a zero, podemos encontrar a relação entre as forças BC e CD
Ao igualar a soma das forças na direção y a zero, podemos determinar as forças BC e CD
Umas vez que as forças BC e CD são iguais
A seguir, vamos analisar a junta B para determinar as forças nos membros AB e BD
Recoloque AB com seu valor
Passo 3
Finalmente, vamos isolar e desenhar o diagrama de corpo livre do membro DEF
Observe que a distância entre os pontos A e F é igual à distância entre os pontos B e D
Uma vez que o membro DF faz com o ângulo horizontal de 15°, ele faz com o ângulo vertical de 75 ∘, ou seja, 105 ∘
Usando a regra do cosseno, calcularemos a distância entre os pontos A e E
Usando a regra do seno, podemos determinar o ângulo β que a mola faz com o membro DEF
Recoloque AE como seu valor
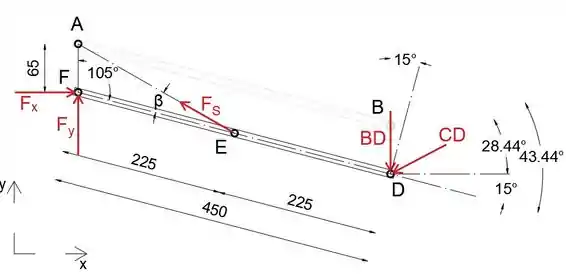
Passo 4
Equacionando a soma dos momentos sobre o ponto F a zero, podemos determinar a força FS
Substitua β, BD e CD por seus valores
Finalmente, a força da mola necessária para manter o sistema em equilíbrio é: