Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 6.6 - Ex. 138
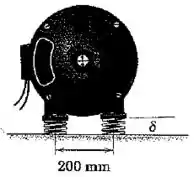
O motor elétrico apresentado está fornecendo a para uma bomba a qual aciona. Calcule o ângulo por meio do qual o motor se inclina sob a ação da carga, se a rigidez de cada uma de suas quatro molas de suporte é de . Em que direção o eixo do motor gira?
Passo 1
Vamos começar entendendo como o ângulo vai aparecer na nossa conta.
Suponha que o motor se incline para um dos lados, de modo que uma das molas seja comprimida em e a outra seja esticada em :
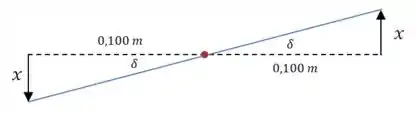
Nesse caso:
Ou seja, nosso objetivo é encontrar a distorção que a mola sofre.
Como nós conhecemos a rigidez de cada uma delas, só precisamos conhecer a força adicional que age sobre cada uma quando o motor se entorta:
Passo 2
Beleza, então temos que encontrar essa força .
Quando o motor se entortar para um dos lados, a mola comprimida fará força para cima, e a mola esticada fará uma força de mesmo módulo para baixo:
Além disso, temos o momento , que é a reação da bomba ao torque que o motor imprime sobre ela.
pode ser calculado a partir da potência e da velocidade angular dadas no enunciado:
Portanto, se o motor faz a bomba rodar no sentido horário, ele se inclina no sentido anti-horário, e vice-versa.
Passo 3
Agora vamos olhar para a soma dos momentos das forças em relação ao ponto quando o motor está em equilíbrio em uma posição inclinada por um ângulo :
Além do momento , o par de forças e separadas por formarão um binário na direção oposta:
E multiplicamos por dois para considerar o par de forças traseiro e o dianteiro.
Substituindo na nossa fórmula de cima:
E se, conforme o desenho do enunciado, o motor se inclina no sentido anti-horário, isso quer dizer que ele está “empurrando” a bomba no sentido horário, e então é nessa direção que seu eixo está girando.
Resposta
O motor se inclina por um ângulo , e o seu eixo gira no sentido horário.