Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 14.Problemas - Ex. 61

A água escoa continuamente entre duas placas A e B com uma velocidade v de intensidade 30 m/s. O jato é dividido em duas partes por uma placa lisa horizontal C. Sabendo que as vazões em cada uma das correntes resultantes são, respectivamente, Q 1 = 100   L /min e Q 2 = 500 L /min, determine (a, Passo 2 ) o ângulo θ , (b, Passo   3 ) a força total exercida pelo jato sobre a placa horizontal.

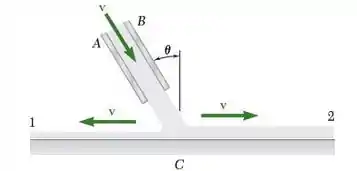
Passo 1

E aí, ferinha!?! Tudo blz? Neste exercício devemos determinar (a) o ângulo de um jato de água e (b) a força total exercida pelo jato sobre uma placa horizontal.

Assumiremos que as velocidades das correntes de água são constantes, logo

v = v ( s e n θ i - c o s θ j )

v 1 = - v i

v 2 = v i

Chamaremos a força que a placa horizontal exerce sobre o fluido de P j

∆ m v + P j ∆ t = ∆ m 1 v 1 + ∆ m 2 v 2

P j = ∆ m 1 ∆ t v 1 + ∆ m 2 ∆ t v 2 - ∆ m ∆ t v

P j = d m d t 1 ( - v i ) + d m d t 2 ( v i ) - d m d t v ( s e n θ i - c o s θ j )

P j = - ρ Q 1 v i + ρ Q 2 v i - ρ Q v ( s e n θ i - c o s θ j )

Resolvendo para os componentes i e j :

i : 0 = - ρ Q 1 v + ρ Q 2 v - ρ Q v s e n θ → Q s e n θ = Q 2 - Q 1

j : P = ρ Q v c o s θ

Passo 2

a) A partir dos cálculos mostrados no Passo 1 , temos:

Q s e n θ = Q 2 - Q 1

s e n θ = 8,3333 × 10 - 3 - 1,667 × 10 - 3 10 × 10 - 3

θ = 41,8 °

Passo 3

b)

P = ρ Q v c o s θ

P = ( 1000 ) ( 10 × 10 - 3 ) ( 30 ) c o s 41,8 °

P = 224   N

Resposta

(a) 41,8 °

(b) 224   N

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

14.44. Três esferas, cada uma de massa m, podem deslizar livremente sobre uma superfície horizontal sem atrito. As esferas A e B estão ligadas por um fio inextensível e inelástico de comprimento l e e
14.45. Um veículo espacial de 360 kg deslocando-se com velocidade v0 (450 m/s)k passa pela origem O. Cargas explosivas dividem, então, o veículo em três partes, A, B e C, com massas de 60 kg, 120 kg e
14.54. Para o jogo de bilhar do Problema 14.53, considere agora que v0 5 m/s, vC 3 m/s e c 1.200 mm. Determine (a) as velocidades vA e vB das bolas A e B, (b) o ponto Aonde a bola A atinge a lateral d
14.53. Em um jogo de bilhar, a bola A tem velocidade inicial v0 ao longo da direção do eixo longitudinal da mesa. Ela atinge a bola B e a seguir a bola C, que estão ambas em repouso. Observa-se que as
14.109. Um bloco B de 7,5 kg está em repouso e uma mola de constante k 15.000 N/m é mantida comprimida em 75 mm por um cordão. Em seguida, o bloco A de 2,5 kg é colocado defronte à extremidade da mola