Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 3.6 - Ex. 111
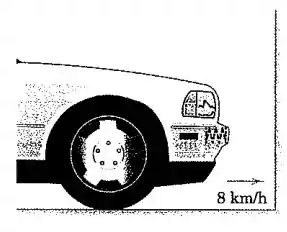
No projeto de um para-choque sobre molas para um carro de , deseja-se parar o carro a partir de uma velocidade de em uma distância igual a de deformação da mola. Especifique a rigidez necessária para cada uma das duas molas por trás do para-choque. As molas estão sem deformação no início do impacto.
Passo 1
Pessoal, vamos lembrar que o trabalho total realizado sobre um corpo é igual à variação de sua energia cinética.
Lembre-se também que o trabalho realizado por uma mola é:
Nesse caso, o trabalho será realizado por duas molas, então:
Passo 2
Vamos manipular a equação obtida a fim de isolar a constante :
Lembre-se que devemos ter e , além de e :
Resposta
Exercícios de Livros Relacionados
Utilize como referência a figura do Prob. 3/105. Sabe-se que o carrinho de 3k g passa sobre o topo da pista e chega em B com uma velocidade v B = 6m / s , determine o trabalho realizado pelo atrito en
A mola está sem deformação na posição x = 0 . Sob a ação de uma força P , o carrinho se desloca da posição inicial x 1 = - 150m m até a posição final x 2 = 80m m . Determine(a) o trabalho realizado so
Utilize o método de trabalho-energia para desenvolver uma expressão para a altura máxima atingida por um projétil que é lançado com velocidade inicial v 0 a partir do nível do solo. Avalie sua express
O guindaste sobre esteiras equipado para demolição está se deslocando a uma velocidade constante de 3k m / h quando é subitamente parado. Calcule o ângulo θ máximo por meio do qual o cabo da bola de d
O carro está se deslocando com a velocidade v 0 = 105k m / h para cima na inclinação de 6 % , e o motorista aciona os freios no ponto A , provocando a derrapagem de todas as rodas. O coeficiente de at