Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 6.8 - Ex. 191

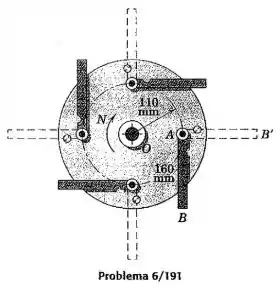
O projeto preliminar de uma unidade para reduzir automaticamente a velocidade de um conjunto que gira livremente é apresentado. Inicialmente a unidade está girando livremente em torno de um eixo vertical através de O a uma velocidade de 600   r p m com os braços fixos nas posições indicadas por A B . Quando os braços são liberados, eles giram para fora e ficam presos nas posições tracejadas mostradas. O disco tem uma massa de 30   k g , com um raio de giração de 90   m m em relação a O . Cada braço tem um comprimento de 160   m m e uma massa de 0,84   k g e pode ser considerado como uma haste esbelta uniforme. Determine a nova velocidade N de rotação e calcule a perda ∆ E de energia do sistema. Os resultados seriam afetados pelo sentido da rotação ou pela sequência de liberação das hastes?

Passo 1

O problema pode ser simplificado se analisarmos apenas um dos braços e em seguida generalizarmos para os outros três. Trabalhando sobre o braço AB, o problema se resume a seguinte figura:

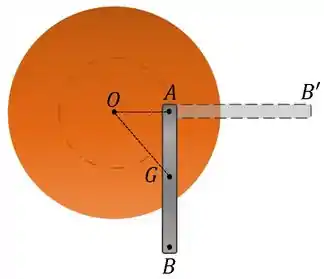
Na configuração inicial, o momento de inércia com relação ao centro O do disco para cada braço é dado por

I o b r a ç o 1 = I - + m d   ²

Por geometria, d é a hipotenusa do triângulo formado por O A - e O G - , conforme figura abaixo

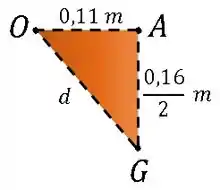
Aplicando o teorema de Pitágoras, temos

d 2 = 0,11 2 + 0,08 2                 ∴                   d = 0,136   m

Retomando a equação de momento de inércia para o braço,

I o b r a ç o 1 = 1 12 0,84 0,16 2 + 0,84 0,136 2 = 0,01733   k g × m 2

Ainda na configuração inicial, o momento de inércia do disco com relação ao seu centro O é dado por

I o d i s c o =   I - = m k 2 = 30 0,09 2 = 0,243   k g × m 2

Passo 2

Na configuração final, a barra ocupa a posição A B ' . Novamente calcularemos os momentos de inércia para o disco e para a nova posição da barra com relação ao centro O do disco.

I o b r a ç o 2 = I - + m d   ²

Daí,

I o b r a ç o 2 = 1 12 0,84 0,160 2 + 0,84 0,11 + 0,08 2 = 0,0321   k g × m 2

O momento de inércia com relação ao disco permanece o mesmo:

I o d i s c o = 0,243   k g × m 2

Passo 3

Pela conservação da quantidade de movimento angular, temos

H o 1 = H o 2

O que resulta em

4 × I o b r a ç o 1 + I o d i s c o ω 1 = 4 × I o b r a ç o 2 + I o d i s c o × ω 2

( 4 × 0,01733 + 0,243 ) 600 × 2 π 60 = ( 4 × 0,0321 + 0,243 ) ω 2

Resolvendo para ω 2 , achamos

ω 2 = 52,8   r a d / s               ∴                   N = 52,8 × 60 2 π =   504,20   r p m

Passo 4

A perda de energia ∆ E do sistema é dada por

∆ E = -   ∆ T

Na configuração inicial, a energia cinética é dada por

T 1 = ∑ 1 2 I o ω 2 = 1 2 4 × 0,01733 + 0,243 600 × 2 π 60 2 = 616,49   J

Na configuração final a energia cinética é dada por

T 2 = ∑ 1 2 I o ω 2 = 1 2 4 × 0,0321 + 0,243 52,8 2 = 517,70   J

Daí, a perda de energia é dada por

∆ E = 616,49 - 517,70 =   98,79   J

Resposta

N = 504,20   r p m

∆ E = 98,79   J

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um elemento de máquina de 200 lb apoiado por quatro molas, cada uma com k = 12 lb / ft constante, é submetido a uma força periódica de frequência 0,8 Hz e amplitude de 20 lb. Determine a amplitude da
Desenhe o análogo elétrico do sistema mecânico mostrado. (Dica: desenhe os loops correspondentes aos corpos livres m e A.)
No Problema, determine o valor necessário da constante decada mola se a amplitude da vibração em regime permanente deveser de 0,4 mm.
Escreva as equações diferenciais definindo (a) os deslocamentos da massa me do Ponto A, (b) as cargas nos capacitores do análogo elétrico
Dois blocos A e B, cada um com massa m, são apoiados como mostrado por três molas da mesma constante k. Os blocos A e B são conectados por um painel de instrumentos e o bloco B é conectado ao solo por