Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 6.8 - Ex. 192

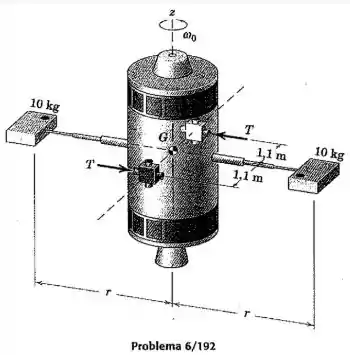
Dois pequenos jatos de empuxo variável são acionados para manter a velocidade angular da nave espacial em relação ao eixo z constante em ω o = 1,25   r a d / s , enquanto as duas hastes telescópicas são prolongadas de r 1 = 1,2   m até r 2 = 4,5   m a uma taxa constante durante um período de 2   m i n . Determine o empuxo necessário T para cada jato como uma função do tempo, onde t = 0 é o instante de tempo em que a ação de prolongamento é iniciada. Os pequenos módulos de experimentos com 10   k g nas extremidades das hastes podem ser tratados como partículas, e a massa das hastes rígidas é desprezível.

Passo 1

A quantidade de movimento angular é dada por

H =   I o ω o + 2 m r 2 ω o

Derivando com relação ao tempo, obtemos

H ˙ =   4 m r r ˙ ω o

Segundo o enunciado, as hastes telescópicas são prolongadas a uma taxa constante de r 1 até r 2 , sendo

r = r 1 + ∆ r ∆ t × t = r 1 + 4,5 - 1,2 120 × t = 1,2 + 0,0275 t

E a taxa de variação de r em relação a t é dada por

r ˙ = 0,0275   m / s

Passo 2

Utilizando a relação Momento-Quantidade de movimento angular, ficamos com

M = H ˙ = 4 m r r ˙ ω o  

De onde tiramos que

2 × T × 1,1 = 4 ( 10 ) ( 1,2 + 0,0275 t ) ( 0,0275 ) ( 1,25 )

Resolvendo para T , obtemos

T = 0,75 + 0,01719 t   N

Resposta

T = 0,75 + 0,01719 t   N

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

No caso de amortecimento subcrucial, os deslocamentos x 1 , x 2 , x 3 mostrados na Fig. 19.11 podem ser considerados iguais aos deslocamentos máximos. Mostre que a razão de dois deslocamentos máximoss
O bloco A pode se mover sem atrito na fenda como mostrado nafigura e sobre ele atuar uma força vertical periódica de intensidade P = P ms e nω ƒ t ƒ , onde ω ƒ = ƒ 2 rad /s e P m = 20 N. Uma mola de c
Um pequeno reboque e sua carga têm uma massa total de 250 kg.O reboque é suportado por duas molas, cada uma de constante10 kN/m, e puxado sobre uma estrada cuja superfície pode ser aproximada por uma
Desenhe o análogo elétrico do sistema mecânico mostrado. (Dica: desenhe os loops correspondentes aos corpos livres m e A.)
Expresse em termos de L, C e E a faixa de valores da resistência R para a qual as oscilações ocorrerão no circuito mostrado quando a chave S for fechada.