Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 6.8 - Ex. 206

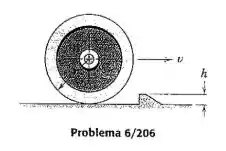
Determine a velocidade mínima v que a roda deve possuir para conseguir rolar por cima da obstrução. O raio de giração centroidal da roda é k , e se supõe que a roda não deslize.

Passo 1

Considere A o ponto da superfície da roda que entra em contrato com a obstrução.

Antes do impacto, a quantidade de movimento angular de A é dada por

H A = I - ω + m v r - h = m k 2 v r + m v r - h = m v k 2 r + r - h

No instante logo após o impacto, temos

H A ' = I A v ' r = m k 2 + r 2 v ' r

Passo 2

Pela conservação da quantidade de movimento angular, temos

H A = H A '

m v k 2 r + r - h = m k 2 + r 2 v ' r

Simplificando e resolvendo para v ' , obtemos

v ' = v 1 - r h k 2 + r 2

Passo 3

Durante o impacto, quando a roda está no pico da obstrução, pelo princípio da conservação da energia mecânica, temos

∆ T + ∆ V g = 0

0 - 1 2 m k 2 + r 2 v ' r 2 + m g h - 0 = 0

Resolvendo para v ' , obtemos

v ' = r 2 g h k 2 + r 2 2

Passo 4

Por fim, igualando as duas expressões encontradas para v ' e resolvendo para v , achamos

v = r k 2 + r 2 - r h 2 g h ( k 2 + r 2 ) 2

Resposta

v = r k 2 + r 2 - r h 2 g h ( k 2 + r 2 ) 2

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O bloco mostrado na figura é abaixado em 30 mm da sua posiçãode equilíbrio e então liberado. Sabendo que depois de 10 ciclos odeslocamento máximo do bloco é de 12,5 mm, determine (a) o fatorde amortec
A suspensão de um automóvel pode ser aproximada pelo sistema simplificado de mola e painel mostrado. (a) Escreva a equação diferencial que define o deslocamento vertical da massa m quando o sistema se
Para uma vibração em estado estacionário com amortecimento sob uma força harmônica, mostre que a energia mecânica dissipada por ciclo pelo painel é E = π c x m 2 ω f , onde c é o coeficiente de amorte
Se um pêndulo simples ou composto for usado para determinar experimentalmente a aceleração da gravidade g, haverá dificuldades. No caso do pêndulo simples, a corda não é realmente sem peso, enquanto n
Resolva o Problema 19.168, supondo que um dashpot de constante c = 6500 N⋅s / m seja introduzido entre o motor e o solo.19.168 - Um motor de 400 kg apoiado por quatro molas, cada uma com 150 kN / m co