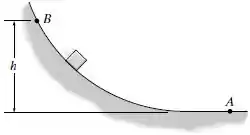
Prove que se o bloco é solto do repouso no ponto de uma trajetória lisa de formato arbitrário, a velocidade que ele alcança quando chega ao ponto é igual à velocidade que ele alcança quando cai livremente de uma altura ; ou seja, .
Passo 1
O enunciado nos dá as seguintes condições:
Bloco solto do repouso ();
Trajetória lisa (força de resistência à tração pode ser desprezada);
Trajetória com formato arbitrário;
Velocidade em igual a ;
.
Como o corpo está indo sentido ponto A, escolheu-se e .
Para mostrar que , inicialmente desenhamos o diagrama de corpo livre do bloco para uma trajetória qualquer usando a imagem fornercida pelo enunciado como referência.
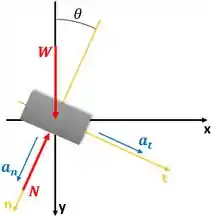
Também sabemos que
Onde é o raio de curvatura no ponto onde o corpo está localizado, é a massa do bloco e é a aceleração gravitacional ( m/s2).
Como a trajetória é aleatória, não temos dados suficientes para encontrar e . Portanto iniciaremos nossa análise através de .
Passo 2
Primeiramente, vamos utilizar a Equação do Movimento no sentido do eixo tangencial.
Sabemos que
Porém, também sabemos que
Onde é o espaço percorrido pelo bloco. Logo,
Igualandao os valores de , obtemos:
Passo 3
Agora iremos resolver a equação encontrada. Ela é uma EDO linear homogênea de 10 ordem e pode ser resolvida pelo método de equações separáveis.
Não conhecemos , portanto devemos relacionar este valor com algo que conhecemos. Neste caso, conhecemos a altura, portanto iremos relacionar com . Voltando no Diagrama de corpo livre, vemos a seguinte relação
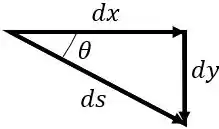
Onde
Logo,
Agora iremos resolver esta EDO
Resposta
Ei, a resposta está no passo a passo :)