Enunciado
Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 10.Problemas - Ex. 2
10.2 Duas barras rígidas AC e BC são conectadas por um pino em C como mostra a figura. Sabendo que a mola de torção em B tem uma constante K, determine a força crítica para o sistema.
Passo 1
Galerinha, vamos ver os dados que temos para usarmos as fórmulas e realizar nosso cálculo:
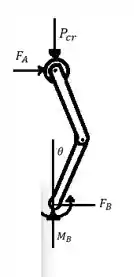
Deixe ser a variação do ângulo de cada barra.
AC.
Resposta
Então gurizada, como acabamos de calcular, temos a resposta de
Exercícios de Livros Relacionados
Sabendo-se que a mola em A é de constante k e que a barra AB é rígida, determinar a carga crítica PCR
Duas barras rígidas AC e BC são conectadas a uma mola de constante k, como mostrado. Sabendo-se que a mola pode atuar tanto a tração quanto a compressão, determinar a carga crítica Pcr para o sistema.
A barra rígida AD é fixa a duas molas de constante k e está em equilíbrio na posição mostrada. Sabendo-se que as cargas P e P' são iguais e opostas e permanecem verticais, determinar a intensidade PCR
Sabendo-se que a mola torcional em B em A é de constante k e que a barra AB é rígida, determinar a carga crítica PCR
A barra rígida AB é fixa a uma articulação em A e duas molas, cada uma de constante k=260kN/m. Se h=0,75m, determinar a carga crítica. Cada uma das molas pode atuar tanto a tração quanto a compressão.