Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 3.4 - Ex. 63
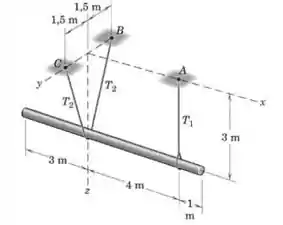
O eixo horizontal de aço tem uma massa de e está suspenso por um cabo vertical em e por um segundo cabo que passa por baixo do eixo e está situado em um plano vertical transversal. Calcule as forças trativas e nos cabos.
Passo 1
Vamos começar considerando o equilíbrio dos momentos. Precisamos escolher um eixo de referência para calcular esse momento de forma que alguma variável desconhecida suma da equação!
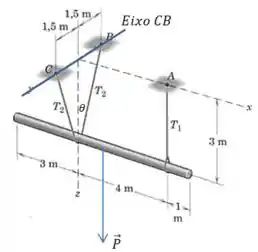
O eixo que passa pelos pontos e é uma boa opção, porque o momento de em relação a ele se anula, já que a linha de ação das forças cruza esse eixo:
Então ficamos com a seguinte expressão:
E o sinal negativo aparece antes de porque ele favorece a rotação no sentido contrário ao da tração.
Passo 2
Beleza, ainda falta a tração . Dessa vez vamos usar o equilíbrio das forças na direção vertical (eixo ). Perceba que o sentido positivo de é para “baixo”.
Vamos então escrever as componentes das forças na direção :
E para escrever as componentes das duas forças de módulo vamos precisar daquele ângulo que desenhamos na figura:
Então a equação do equilíbrio vai ficar assim:
E então:
Passo 3
Agora só precisamos calcular o ângulo . Olhando para a figura que desenhamos no passo podemos escrever o seguinte:
Substituindo na nossa expressão para :
Resposta
As forças são e .