Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 6.Problemas Revisão - Ex. 149

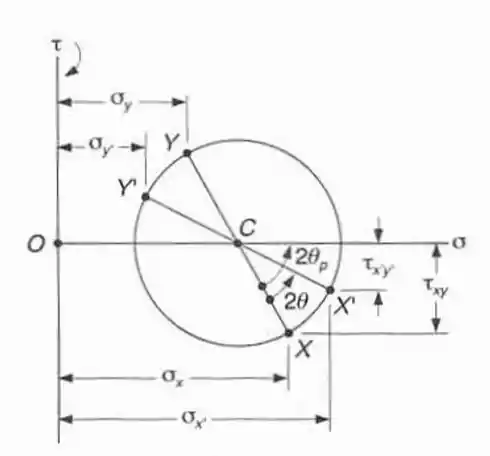
O círculo de Mohr mostrado corresponde ao estado de tensões dado nas Figs. 6.5a e b, Sec. 6.1. Notando que σ x ' = O C ' - C X ' cos ⁡ 2 θ p - 2 θ e que τ x ' y ' = C X ' s e n ( 2 θ p - 2 θ ) , desenvolver as expressões σ x ' e τ x ' y ' , dadas nas Eqs. (6.5) e (6.6), respectivamente. (Sugestão: Usar s e n A + B = s e n A ⋅ cos ⁡ B + cos ⁡ A ⋅ s e n ( B ) e cos ⁡ A + B = cos ⁡ A ⋅ cos ⁡ B - s e n A ⋅ s e n ( B ) .)

Passo 1

Bom, primeiro a questão fala para chegar à duas equações, vamos enuncia-las aqui. A primeira que trata sobre a tensão normal é:

σ x ' = σ x + σ y 2 + σ x - σ y 2 ⋅ cos ⁡ 2 θ + τ x y ⋅ s e n 2 θ                     [ E q   6.5 ]

Já a segundo trata da tensão cisalhante:

τ x ' y ' = - σ x - σ y 2 ⋅ s e n 2 θ + τ x y ⋅ cos ⁡ 2 θ                                 [ E q   6.6 ]

Então para chegar a essas equações a gente vai ter que sair dosestado X e chegar no estado X ' . Para isso vamos utilizar a geometria do círculo e um pouco de trigonometria.

Passo 2

Vamos achar o centro e o raio do ciclo de Mohr:

σ m é d = σ x + σ y 2

R = σ x - σ y 2 2 + τ x y 2 2

Como não foram fornecidos dados numéricos vamos deixar assim.

É importante ver que o ciclo não muda, o que muda é que ocorre uma rotação de X para X ' , dessa forma o σ m é d e o R permanecem iguais. Assim, podemos deduzir alguns termos, como:

O C ' : este termo é exatamente igual à O C que por sua vez vale:

O C ' = O C = σ m é d = σ x + σ y 2

C X ' : este termo irá valer:

C X ' = R ⋅ cos ⁡ 2 θ p - 2 θ

O problema forneceu o seguinte dado:

σ x ' = O C ' - C X ' cos ⁡ 2 θ p - 2 θ

Daí a gente tem que perceber, substituindo os valores de O C ' e C X ' , que

σ x ' = O C ' - C X ' cos ⁡ 2 θ p - 2 θ

É igual a

σ x ' = σ x + σ y 2 - R ⋅ cos ⁡ 2 θ p - 2 θ cos ⁡ 2 θ p - 2 θ

σ x ' = σ x + σ y 2 ⋅ cos ⁡ 2 θ p - 2 θ - R ⋅ cos 2 ⁡ 2 θ p - 2 θ

Passo 3

Agora vamos utilizar a propriedade trigonométrica:

cos ⁡ A + B = cos ⁡ A ⋅ cos ⁡ B - s e n A ⋅ s e n ( B )

cos ⁡ 2 θ p - 2 θ = cos ⁡ 2 θ p ⋅ cos ⁡ 2 θ + s e n 2 θ p ⋅ s e n ( 2 θ )

Galera, agora a gente vai recorrer para a geometria do ciclo e ao ângulo 2 θ p , observando o ciclo vamos ver que:

sen ⁡ 2 θ p = τ x y R

cos ⁡ 2 θ p = σ x - σ m é d R

Agora podemos simplificar um pouco a relação:

cos ⁡ 2 θ p - 2 θ = cos ⁡ 2 θ p ⋅ cos ⁡ 2 θ + s e n 2 θ p ⋅ s e n ( 2 θ )

Que ficará da forma:

cos ⁡ 2 θ p - 2 θ = σ x - σ m é d R ⋅ cos ⁡ 2 θ + τ x y R ⋅ s e n ( 2 θ )

Vamos precisar também do termo..

cos 2 ⁡ 2 θ p - 2 θ = cos ⁡ 2 θ p ⋅ cos ⁡ 2 θ + s e n 2 θ p ⋅ s e n ( 2 θ ) 2  

cos 2 ⁡ 2 θ p - 2 θ = σ x - σ m é d R ⋅ cos ⁡ 2 θ + τ x y R ⋅ s e n 2 θ 2

Esse termo será igual a:

σ x - σ m é d R 2 ⋅ cos 2 ⁡ 2 θ + 2 × τ x y ( σ x - σ m é d ) R 2 ⋅ cos ⁡ 2 θ s e n 2 θ + τ x y R 2 ⋅ s e n ² 2 θ

Ficou meio grande né? Vamos continuar no próximo passo =D

Passo 4

Ok, respira funda e vamos lá... A gente tinha aquela equação grandona, para facilitar vamos olhar o seguinte termo

σ x - σ m é d

Mas a tensão média é calculada como:

σ m é d = σ x + σ y 2

Então a gente pode ver que:

σ x - σ m é d = σ x - σ x + σ y 2 = σ x - σ y 2

Substituindo na nossa equação:

σ x - σ y 2 R 2 ⋅ cos 2 ⁡ 2 θ + 2 × τ x y ( σ x - σ y ) ( 2 R ) 2 ⋅ cos ⁡ 2 θ s e n 2 θ + τ x y R 2 ⋅ s e n ² 2 θ

A gente pode fazer a mesma coisa com o termo:

cos ⁡ 2 θ p - 2 θ = σ x - σ m é d R ⋅ cos ⁡ 2 θ + τ x y R ⋅ s e n ( 2 θ )

E obter:

cos ⁡ 2 θ p - 2 θ = σ x - σ y 2 R ⋅ cos ⁡ 2 θ + τ x y R ⋅ s e n ( 2 θ )

Pessoal, lembrem que a gente quer σ x ' , então a gente vai ter que substituir os dois termos nessa equação aqui de baixo:

σ x ' = σ x + σ y 2 ⋅ cos ⁡ 2 θ p - 2 θ - R ⋅ cos 2 ⁡ 2 θ p - 2 θ

Pessoal, observem que os termos cos ⁡ 2 θ p - 2 θ ; cos 2 ⁡ 2 θ p - 2 θ e R todos podem ser escritos em função de σ x , σ y , τ x y e 2 θ . Sendo assim daqui para frente o problema se torna unicamente algébrico e fica muito extenso para ser colocado nessa resolução.

O mais importante nós já fizemos, que é expressar tudo em função dos termos “finais”.

Passo 5

Para τ x ' y ' vamos utilizar:

τ x ' y ' = C X ' s e n ( 2 θ p - 2 θ )

O desenvolvimento será muito parecido, tendo em vista que os mesmos termos 2 θ p e C X ' são utilizados. A única diferença é a utilização da relação trigonométrica para o senos ao invés dos cossenos:

s e n A + B = s e n A ⋅ cos ⁡ B + cos ⁡ A ⋅ s e n ( B )

Valeu, galera um grande abraço!!!

Resposta

Ei, a resposta está no passo a passo :)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A barra BD feita de aço (E = 200G P a ) é utilizada para contenção lateral da haste comprimida ABC. O máximo esforço que se desenvolve em BD é igual a 0,02P. Se a tensão não deve exceder 124,1 MPa e a
O cabo BC de 4 mm de diâmetro é feito de um aço com E = 200G P a . Sabendo que a máxima tensão no cabo não pode exceder 190 MPa e que a deformação do cabo não deve exceder 6 mm, determine a máxima for
Um tubo de alumínio com 250 mm de comprimento (E = 70G P a ) , 36 mm de diâmetro externo de 28 mm de diâmetro interno pode ser fechado em ambas as extremidades por meio de tampas com rosca simples de
Ambas as partes da barra ABC são feitas de um alumínio para o qual E = 70G P a . Sabendo que a intensidade de P é 4 kN, determine (a) o valor de Q e modo que o deslocamento em A seja zero e (b) o desl
O comprimento do fio de aço CD de 3 32 in diâmetro foi ajustado de modo que, sem nenhuma força aplicada, existe um espaço de 1 16 i n entre a extremidade B da barra rígida ACB e um ponto de contato E.