Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 6.Problemas - Ex. 142b

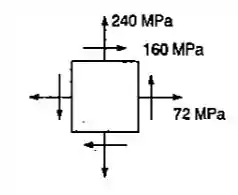
O estado plano de tensões mostrado é conhecido na superfície de um componente de máquina, feito de aço de alta resistência. Sabendo-se que E = 200   G P a e G = 80 G P a , determinar a orientação e a intensidade das três deformações específicas normais principais: (a) pela determinação do correspondente estado de deformação. (Usar a Eq. (2.43), e Eqs. (2,38)); e então, usar o círculo de Mohr para a deformação; (b) Usando ocírculo de Mohr para tensões, determinar os planos principais e as tensões principais; e então, determinar as correspondentes deformações normais.

Passo 1

Primeiramente para resolver esse exercício é necessário saber identificar corretamente as tensões:

σ x = 72   M P a

σ y = 240   M P a

τ x y = 160   M P a

Depois vamos achar o coeficiente de Poisson de modo a fazer corretamente o círculo de Mohr.

Passo 2

Para achar o coeficiente de Poisson a gente vai utilizar a equação:

G = E 2 ⋅ ( ν + 1 )

Dessa forma:

ν = E 2 G - 1

ν = 200 2 ⋅ 80 - 1

ν = 0,25

Passo 3

Agora a gente vai ter que construir o ciclo de Mohr para isso vamos descobrir a tensão média e o raio do ciclo.

σ m é d = σ x + σ y 2

σ m é d = 72 + 240 2 = 155   M P a

E o raio é calculado como:

R = σ x - σ y 2 2 + τ x y 2 2

R = 72 - 240 2 2 + 160 2 2

R = 13456

R = 116   M P a

Assim podemos desenhar o ciclo de Mohr:

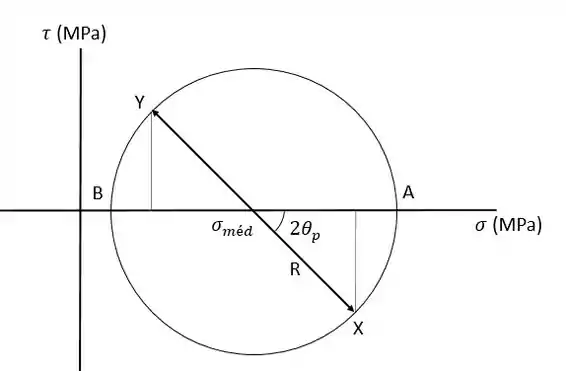
Lembrando que as tensões A e B são as tensões principais e podem ser calculadas como:

σ A = σ m á x = σ m é d + R

σ A = 155 + 116 = 271   M P a

σ B = σ m í n = σ m é d - R

σ B = 155 - 116 = 39   M P a

Passo 4

Show of pelota. Então até aqui estamos seguindo à risca o que a questão pede, que é calcular o ciclo de mohr e achar as tensões principais. Então só falta achar a orientação do plano principal, que é dada pelo ângulo θ p . Vamos fazer isso a partir da geometria do círculo de Mohr!

t g 2 θ p = 2 ⋅ τ x y σ x - σ y

t g 2 θ p = 2 ⋅ 160 72 - 240

t g 2 θ p = - 1,90476

2 θ p = a r c t g - 1,90476 = - 62 °

θ p = - 31 °

Passo 5

Agora só falta achar as deformações principais, com base nas tensões principais e utilizando as equações que o problema pediu, que são:

ε a = 1 E ⋅ ( σ a - ν ⋅ σ b )

ε a = 1 200 × 10 9 ⋅ ( 271 × 10 6 - 0,25 ⋅ 39 × 10 6 )

ε a = 1306   μ

Para ε b

ε b = 1 E ⋅ ( σ b - ν ⋅ σ a )

ε b = 1 200 × 10 9 ⋅ ( 39 × 10 6 - 0,25 ⋅ 271 × 10 6 )

ε b = - 143   μ

Para ε c temos um caso um pouquinho diferente:

ε c = - ν E ⋅ ( σ x + σ y )

ε c = - 0,25 200 × 10 9 ⋅ ( 72 × 10 9 + 240 × 10 9 )

ε c = - 390   μ

Resposta

b)

θ p = 31 °

ε a = 1306   μ

ε b = - 143   μ

ε c = - 390   μ

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O diâmetro da parte central do balão de borracha é d = 100 mm. Se a pressão do ar em seu interior provocar o aumento do diâmetro do balão até d = 125 mm, determine a deformação normal média na borrach
Se a deformação normal for definida em relação ao comprimento final, isto é: em vez de em relação ao comprimento original, mostre que a diferença entre essas deformações é representada como um termo d
Uma haste tem raio de 10mm . Se estiver sujeita a uma carga axial de 15N tal que a deformação axial na haste seja ϵ x = 2,75 ⋅ 10 - 6 , determine o módulo de elasticidade E e a mudança em seu diâmetro
Mostre que, para o caso do estado plano de tensão, a lei de Hooke pode ser expressa como σ x = E 1 - y 2 ∈ x + v ∈ y , σ y = E 1 - y 2 ∈ y + v ∈ x
O eixo tem raio de 15 mm e é feito de aço-ferramenta L2. Determine as deformações nas direções x’ e y’, se for aplicado um torque T = 2 kN.m ao eixo.