Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 16.Problemas - Ex. 141

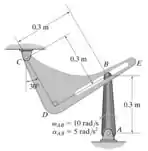
O raio do pino B fixo à manivela AB desliza livremente ao longo da ranhura no membro CDE. Se AB gira com o movimento mostrado, determine a velocidade angular de CDE no instante mostrado.

Passo 1

Antes de iniciarmos a resolução do exercício, vamos colocar os eixos de rotação, x y z , e o eixo fixo, X Y Z . Consideremos que ambos são coincidentes e são colocados em CDE. Então,

v c = 0 ω C D E = ω C D E k

Para o movimento do ponto B com relação ao eixo x y z em relação ao ponto C, teremos:

r B / C = 0,3 2 + 0,3 2   m = 0,3 . 2 i

Passo 2

Calcularemos, agora, a velocidade relativa v r e l x y z . Com isso,

v r e l x y z = v r e l x y z . cos ⁡ 45 ° i + v r e l x y z . sen ⁡ 45 ° j = 0,7071 . v r e l x y z i + 0,7071 . v r e l x y z j

Passo 3

Como a manivela rotaciona em relação ao eixo fixo, então v B , com relação ao eixo X Y Z pode ser calculada. Com isso,

v B = ω A B × r B = 10 k × ( - 0,3 . cos ⁡ 75 ° i + 0,3 . sen ⁡ 75 ° j ) = - 2,898 i - 0,7765 j   m / s

Passo 4

Agora que fizemos os passos anteriores, podemos, finalmente, usar a fórmula de velocidade relativa para encontrar o valor de ω C D E . Então,

v B = v C + ω C D E × r B / C + v r e l x y z

Substituiremos os valores que conhecemos:

Agora iremos igualar as componentes i e j.

Resolvendo as equações acima, vamos chegar em:

v r e l x y z = - 4,098   m / s

ω C D E = 5   r a d / s

Resposta

ω C D E = 5   r a d / s

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um brinquedo em um parque de diversões consiste de um braço em rotação A B que tem uma aceleração angular α A B = 1r a d / s 2 quando ω A B = 2r a d / s no instante mostrado. Também nesse instante o c
As extremidades da barra AB estão confinadas a se deslocarem ao longo das trajetórias mostradas. Em um dado instante, A tem uma velocidade de 2,4 m/s e uma aceleração de 0,9 m/s². Determine a velocida
A argola é lançada na superfície áspera de maneira que ela tem uma velocidade angular ω = 4r a d / s e uma aceleração angular α = 5r a d / s 2 . Além disso, seu centro tem uma velocidade v O = 5m / s
O disco está se deslocando para a esquerda de tal maneira que ele tem uma aceleração angular α = 8r a d / s 2 e velocidade angular ω = 3r a d / s no instante mostrado. Se ele não desliza em A, determi
A argola é lançada na superfície áspera de maneira que ela tem uma velocidade angular ω = 4r a d / s e uma aceleração angular α = 5r a d / s 2 . Além disso, seu centro tem uma velocidade v O = 5m / s