Enunciado
Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 16.Problemas - Ex. 110
O disco está se deslocando para a esquerda de tal maneira que ele tem uma aceleração angular e velocidade angular no instante mostrado. Se ele não desliza em A, determine a aceleração do ponto D.
Passo 1
Começaremos o exercício calculando a aceleração do centro de massa do disco com base na figura a seguir:
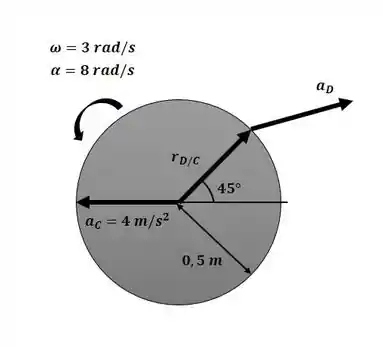
Passo 2
Agora podemos escrever a aceleração no ponto D com o auxílio da figura a seguir:
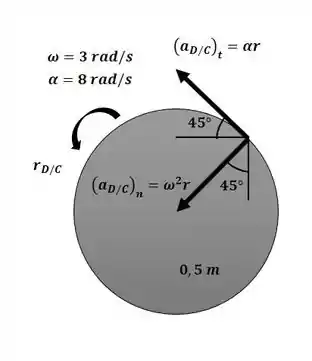
Passo 3
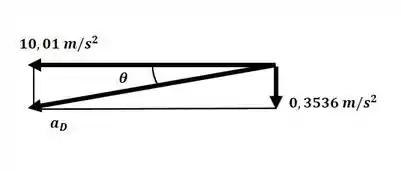
Agora podemos determinar a direção e o módulo da aceleração no ponto D, conforme o esquema a seguir:
Resposta
Exercícios de Livros Relacionados
O movimento do cilindro de 75 mm de raio é controlado pela corda mostrada na figura. Sabendo que a extremidade E da corda tem velocidade de 300 mm/s e aceleração de 480 mm/s2, ambas orientadas para ci
Um tambor de 75 mm de raio está preso rigidamente a um tambor de 125 mm de raio, como mostra a figura. Um dos tambores rola sem deslizar sobre a superfície mostrada e uma corda é enrolada ao redor do
Um tambor de 75 mm de raio está preso rigidamente a um tambor de 125 mm de raio, como mostra a figura. Um dos tambores rola sem deslizar sobre a superfície mostrada e uma corda é enrolada ao redor do
15.144. No instante mostrado na figura, a barra AB gira com uma velocidade angular constante ω e uma aceleração angular α , ambas no sentido horário. Usando o método da Seção 15.9, deduza expressões p
15.143. Um disco de raio r rola para a direita com uma velocidade constante v. Representando por P o ponto do aro em contato com o solo em t 0, deduza expressões para os componentes horizontal e verti