Enunciado
Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 16.Problemas - Ex. 111
A argola é lançada na superfície áspera de maneira que ela tem uma velocidade angular e uma aceleração angular . Além disso, seu centro tem uma velocidade e uma desaceleração . Determine a aceleração do ponto A nesse instante.
Passo 1
Começaremos o exercício calculando as componentes da aceleração no ponto A nesse instante com o auxílio das duas figuras a seguir:
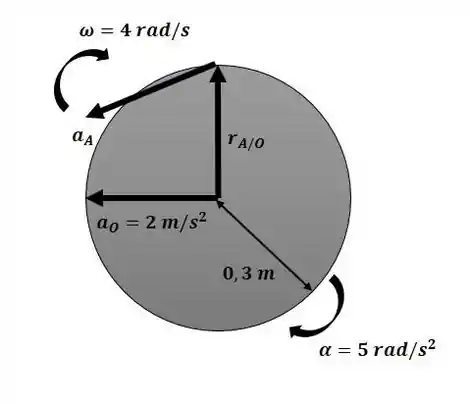
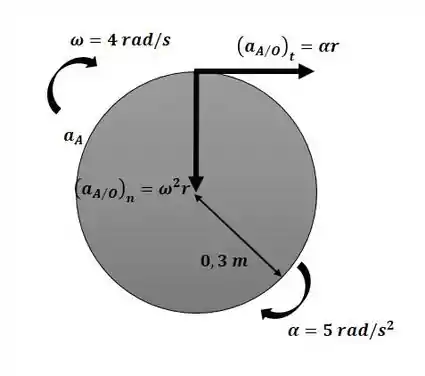
Passo 2
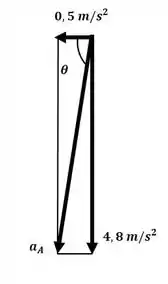
Agora podemos determinar a direção e o módulo da aceleração no ponto A, conforme o esquema a seguir:
Resposta
Exercícios de Livros Relacionados
15.141. A barra AB desloca-se sobre um rolete em C enquanto a extremidade A se move para a direita com uma velocidade constante v A . Usando o método da Seção 15.9, deduza expressões para a velocidade
15.146. A posição da barra AB é controlada por um disco de raio r que está preso no balancim CD. Sabendo que o balancim se desloca verticalmente para cima com velocidade constante v0, deduza uma expre
15.147. No Problema 15.146, deduza uma expressão para a aceleração angular da barra AB.
15.145. No instante mostrado na figura, a barra AB gira com uma velocidade angular constante ω e uma aceleração angular α , ambas no sentido horário. Usando o método da Seção 15.9, deduza expressões p
15.148. Uma roda de raio r rola sem escorregar ao longo do interior de um cilindro fixo de raio R com uma velocidade angular constante . Representando por P o ponto da roda em contato com o cilindro e