Enunciado
Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 19.Problemas - Ex. 12
O volante de 100 kg tem um raio de giração em relação a seu centro de gravidade O de , Se ele gira no sentido anti-horário com uma velocidade angular de 1200 rev/min antes de o freio ser aplicado, determine o tempo necessário para o volante chegar ao repouso quando uma força P = 1000 N for aplicada à alavanca. O coeficiente de atrito cinético entre a correia e a borda do volante é . (Dica: lembre, do texto de estática, que a relação da tração na correia é dada por , onde é o ângulo de contato em radianos.)
Passo 1
Para resolver esse exercício, iremos considerar a aceleração da gravidade .
Começaremos o exercício aplicando o somatório de momento em torno do ponto A com o auxílio da imagem a seguir, e utilizando a relação de tração na correia dada no enunciado para determinar o valor de e :
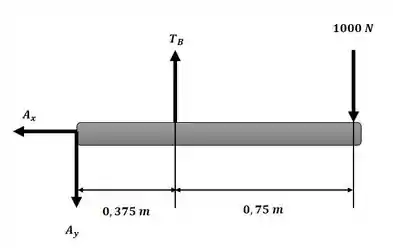
Agora, substituindo esse valor na relação da correia fornecida no enunciado e sabendo que o ângulo de contato vale 180° = radianos, podemos determinar :
Passo 2
Agora, para determinar o tempo necessário para o volante chegar ao repouso, aplicaremos o princípio do impulso e momento angular. Mas antes disso, precisamos calcular o momento de inércia do volante e converter a velocidade angular fornecida para radianos por segundo. Sendo assim:
Agora, convertendo a velocidade angular inicial:
Passo 3
Agora possuímos todos os dados necessário para aplicar o princípio do impulso e do momento angular em torno do ponto O com o auxílio da imagem, sendo assim:
