Enunciado
Mecânica e Resistência dos Materiais - Estatica das Estruturas por Humberto Lima Soriano- Ed: 3º - Capítulo 1.9 - Ex. 3ii
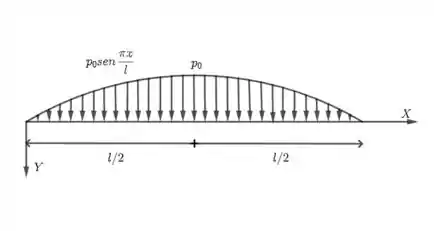
Reduza as forças representadas na figura anterior a origem dos sistemas cartesianos indicados. Idem para as forças distribuídas mostradas na figura que se segue
Passo 1
Como as forças são paralelas, coplanares e distribuída em uma linha no plano , podemos usar a seguinte equação para reduzi-las:
.
Nesse caso, e devemos notar que a força está distribuída numa linha de comprimento . Então, devemos resolver a integral:
Passo 2
Vamos começar fazendo a substituição de variáveis , então . Ou seja, . Além disso, temos que mudar os intervalos de integração: quando , e quando , . Logo,
Como a força aponta no sentido positivo de , então
Passo 3
Devemos aplicar a força encontrada no passo anterior a um ponto dado pela expressão
.
A integral do denominador foi resolvida no passo anterior. Para a integral do numerador, fazemos a mesma mudança de variáveis que anteriormente
Vamos resolver a integral separadamente usando integração por partes.
.
Agora que sabemos que o resultado da integral é , obtemos . Logo, para reduzir as forças representadas na figura, temos que aplicar uma força de módulo no ponto
.
Resposta
Para reduzir as forças, temos que aplicar uma força de módulo no ponto .