Enunciado
Mecânica e Resistência dos Materiais - J. L. Meriam - Estática - Mecânica para Engenharia- Ed: 7º - Capítulo 5.Problemas - Ex. 37
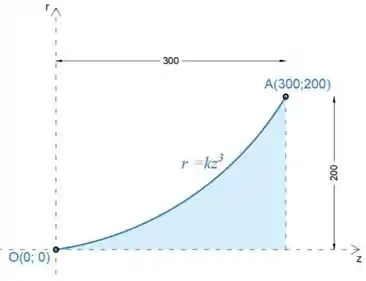
Localize o centro de massa do corpo sólido homogêneo cujo volume é determinado girando a área sombreada em 360 ∘ em torno do eixo z.
Passo 1
Primeiro, precisaremos determinar o coeficiente k. Coloque as coordenadas do ponto A na função r = kz ^ 3 para determinar o coeficiente k
Substituiremos por na função acima
Passo 2
Observe que, como o corpo é homogêneo, o centro de massa e o centróide são iguais.
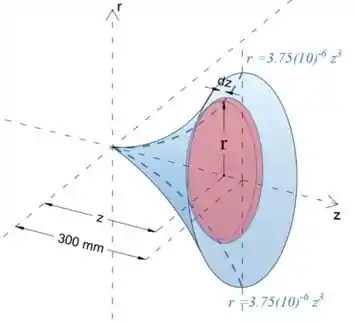
Vamos cortar a área sombreada e isolar a área de volume infinitesimal de espessura d = na distância z de distância do início do sistema de coordenadas.
(1)
A área do círculo isolado é
Como o raio segue a curva , substituiremos por
(2)
Substitua pela expressão (2) na expressão (1)
(1.1)
Passo 3
Integrando a expressão (1.1) ao longo do intervalo [0≤z≤300], obteremos o volume total da figura
substitua pela expressão
Note que e são constantes
Integre o lado direito com relação a
substitua por 300 e por
A expressão para o eixo t do centroide é:
Substitua pela expressão
Note que e são constantes
Integre o lado direito da equação com respeito a
Substitua por 300 e e por seus valores
Passo 4
Por fim, a coordenada s do centroide é:
Observe que, como a área sombreada gira em torno de :z -eixo, seu centróide fica sobre ela.
ou seja,