Enunciado
Mecânica e Resistência dos Materiais - Hibbeler - Estática- Ed: 14º - Capítulo 4.Problemas - Ex. 26
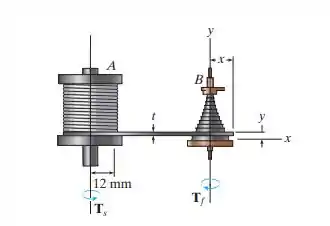
Os relógios antigos eram construídos usando uma polia B em forma de cone para impulsionar as engrenagens e os ponteiros do relógio. A finalidade dessa polia é aumentar a alavanca desenvolvida pela mola principal A enquanto ela se desenrola e, desse modo, perde parte de sua tração. A mola principal pode desenvolver um torque (momento) Ts = ku, onde k = 0,015 N m/rad é a rigidez torsional e u é o ângulo de giro da mola em radianos. Se o torque Tf desenvolvido pela polia tiver de permanecer constante enquanto a mola principal se desenrola, e x = 10 mm quando u = 4 rad, determine o raio exigido da polia quando u = 3 rad.
Passo 1
Oi oi, meu xuxuzinho!! Tudo bem com você?? Como está com essa pandemia?? Preparado para voltar?? Então vamos lá Vamos analisar o que a nossa questão nos pede e matar essa em 10 minutos?? Bora. Bom, nosso enunciado nos pede para analisarmos a figura e dizermos qual a força a partir do eixo. Parece muita coisa, mas é tranquilo. Partiu??
Passo 2
Ok, nosso primeiro passo vai ser lembrar que, numa determinação de momento, cortante e normal, o cortante é positivo pela direita se ele for para baixo, e que a força aplicada deve ser sempre perpendicular à distância para sabermos o momento.
Para um torque com ângulo de temos que:
Eaii?? Chegou bem até aqui?? Então bora substituir os valores e continuar nossa conta.
Passo 3
Pronto!! Agora vamos jogar tudo lá na nossa formulinha e achar nossos valores!!