Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 7.5 - Ex. 3
3. Repita o experimento do problema , mas use um ângulo de rotação pequeno, por exemplo, . Observe as posições finais aproximadamente iguais para as duas sequências distintas de rotação. O que essa observação leva você a concluir a respeito da combinação de rotações infinitesimais e a respeito da derivada no tempo de grandezas angulares? Compare suas observações com a figura .
Passo 1
Primeiramente vamos fazer o esboço da primeira sequência, considerando os giros em e em .
Passo 2
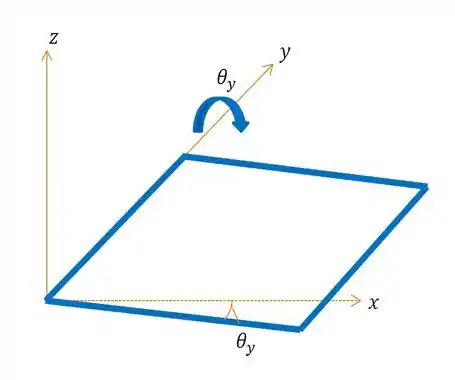
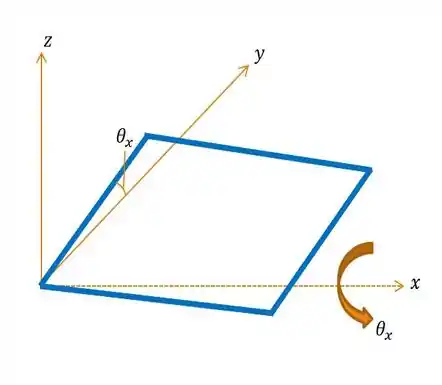
E agora, façamos o esboço da segunda sequência, novamente levando em consideração os giros em e :
Passo 3
Analisando as imagens tanto do como do , temos que quanto menor o ângulo de rotação, maior a semelhança entre as posições finais, de modo que elas tornam-se quase essencialmente iguais. Ou seja, ângulos infinitesimais são adicionados como vetores mais adequados.
Resposta
Concluimos que ângulos infinitesimais são adicionados como vetores mais adequados.