Enunciado
Física - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 8.2 - Ex. 15
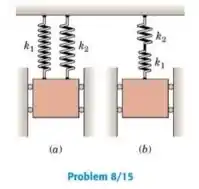
Substitua as molas em cada um dos dois casos representados, por uma única mola de rigidez k (rigidez equivalente da mola), que fará com que cada massa vibre com sua frequência original.
Passo 1
Para determinarmos a relação entre as constantes das molas para os casos (a) e (b), vamos precisar considerar a relação entre as forças de cada mola.
Passo 2
Para a letra (a), como as molas estão em paralelo entre si, as forças podem ser somadas para obter uma força total das molas:
Expressando cada força como força elástica:
Como as variações em torno da posição de equilíbrio são as mesmas para cada mola, os x são iguais, portanto, o x da força equivalente também será.
Simplificando:
Passo 3
No caso da letra (b), as molas estão em série, com isso, a força exercida sobre a mola 1 será igual à força sobre a mola 2, podemos chamar essa força de F:
E o deslocamento do equilíbrio x, pode ser escrito em termos dessas forças
Como a deflexão equivalente é a soma das deflexões:
Ao substituirmos as equações para cada deflexão na equação acima, ficamos com:
Mas como as forças são iguais:
Simplificando: