Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 8.Problemas - Ex. 141
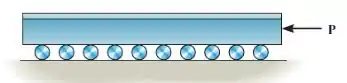
A viga de aço de toneladas é movida sobre uma superfície nivelada usando uma série de roletes com diâmetro de , para os quais o coeficiente de resistência a rolamento é no solo e na superfície inferior da viga. Determine a força horizontal necessária para empurrar a viga para frente em uma velocidade constante. Dica: use o resultado do Problema 8-140.
Passo 1
Galera, quando um cilindro rígido rola com velocidade constante por uma superfície rígida, a força normal exercida pela superfície sobre o cilindro atua perpendicularmente ao ponto de contato. Mas nós sabemos que nenhum material é perfeitamente rígido e, portanto, a reação da superfície sobre o cilindro consiste em uma distribuição de pressão normal. Conforme ele rola, o material da superfície na frente do cilindro retarda o movimento, pois ele está sendo deformado. Para manter esse movimento constante, é necessária uma força motriz horizontal ser aplicada no cilindro.
Para manter o cilindro em equilíbrio, ou seja, manter ele rolando a uma velocidade constante é preciso que seja concorrente com a força motriz e o peso . Assim, temos a seguinte expressão para esse tipo de situação:
Passo 2
Essa questão acaba por ser muito tranquila graças a dica que foi dada no enunciado (valeu, autor!). Na questão anterior, nós demonstramos que a expressão para a força necessária para mover um objeto sujeito a duas resistências de rolamento era igual a:
Assim, como , , e , temos:
Resposta
A força deve ser igual a: