Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 6.Problemas - Ex. 33
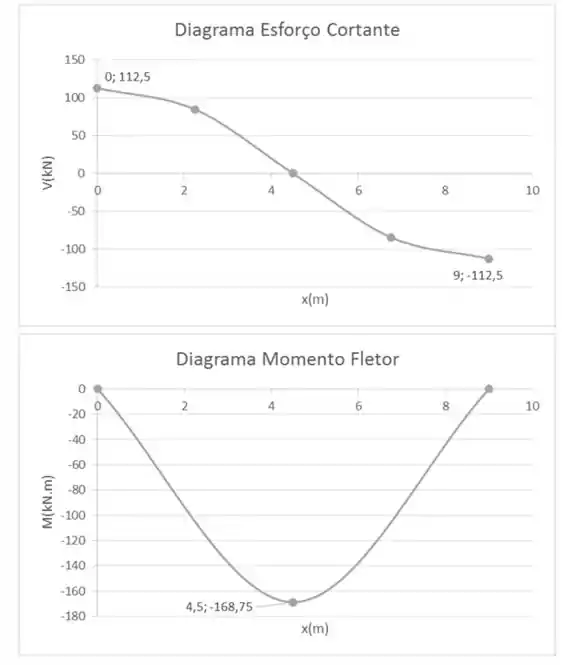
Represente graficamente os diagramas de força cortante e momento fletor para a viga.
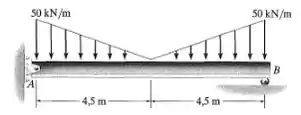
Passo 1
Fala galerinha bonita, tudo belezinha?
Primeiramente, devemos calcular as reações de apoio. Neste caso, devido à simetria, já sabemos que as reações de apoio são iguais e é metade do carregamento total:
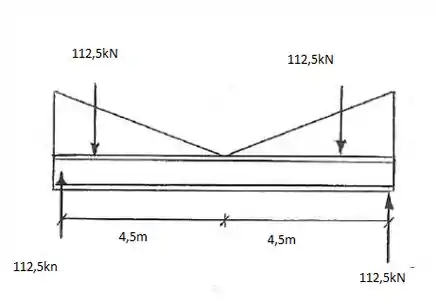
Belezoca, então calculando as reações de apoio, vamos obter que:
Logo:
Agora para , vamos obter que:
Tal que:
Iradoso, agora bora lá escrever as equações dos esforços internos.
Passo 2
Show de bola, agora pra gente escrever as equações de esforços internos vamos dividir a viga em seções, de modo que:
Seção 1, no intervalo vamos obter que:
E para :
Agora para a Seção 2, no intervalo , vamos descobrir que:
Já será:
Com as reações de apoio, podemos fazer os diagramas de cortante e momento fletor, respectivamente:
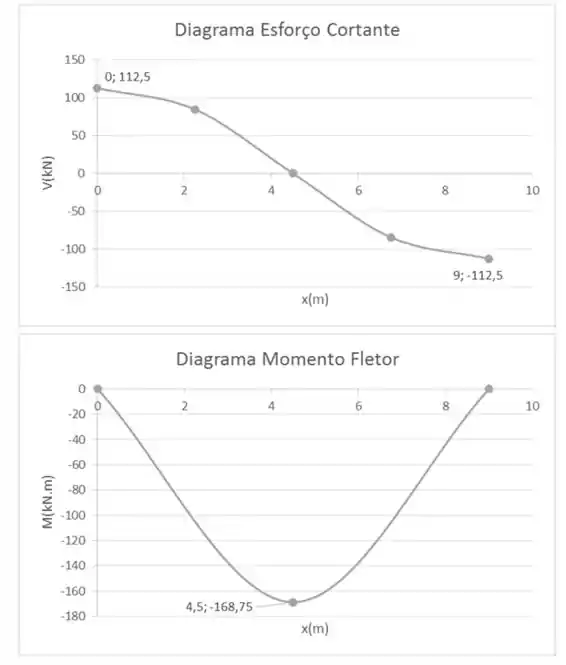
Resposta
