Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 1.Problemas - Ex. 8
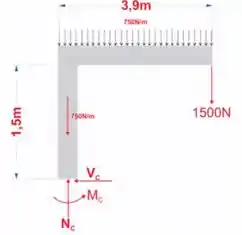
A lança DF do guindaste giratório e a coluna DE têm peso uniforme de 750 N/m. Se o guindaste e a carga pesam 1.500 N, determine as cargas internas resultantes nas seções transversais que passam nos pontos A, B e C.
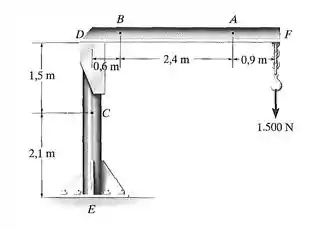
Passo 1
Vamos primeiro fazer o DCL do segmento AF do guindaste
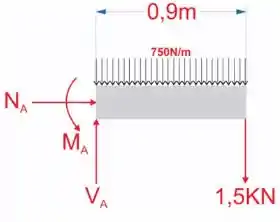
Onde força normal momento
Força cortante
Como podemos ver, ele nos dá a força em N/m. Portanto, para acharmos a resultante desta força basta multiplicar pela área em que ela é aplicada. Ou seja
E o seu ponto de atuação é no metade do retângulo
Passo 2
Agora, vamos utilizar as equações de equilíbrio e momento em relação à seção no ponto
Passo 3
Para o ponto B, é só repetir os passos anteriores
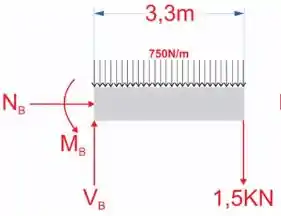
Passo 4
Os passos para o ponto C também se repetem.
Resposta
Exercícios de Livros Relacionados
O dispositivo mostrado na figura sustenta uma força de 80N . Determine as cargas internas resultantes que agem sobre a seção no ponto A .
Determine as cargas internas resultantes que agem na seção transversal no ponto D do elemento AB.
Resolva o Problema 1.6 para as cargas internas resultantes que agem no ponto E.
A viga AB é suportada por um pino em A e por um cabo BC. Determine as cargas internas resultantes que agem na seção transversal no ponto D.
Determine a distância de colocação a do suporte de rolete de modo que o maior valor absoluto do momento seja um mínimo. Represente graficamente os diagramas de força cortante e momento fletor para ess