Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 6.Problemas - Ex. 37
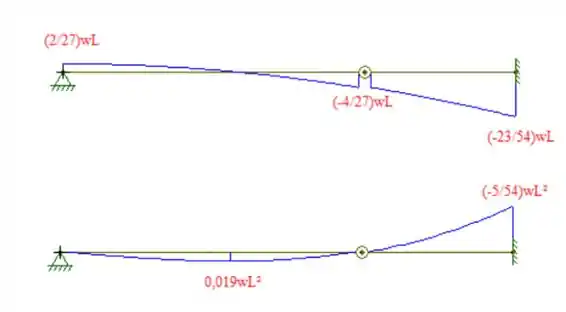
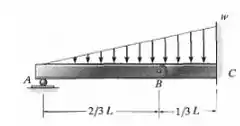
A viga composta consiste em dois segmentos interligados por um pino em . Represente graficamente os diagramas de força cortante e momento fletor se ela suportar a carga distribuída mostrada na figura.
Passo 1
Primeiramente, vamos determinar as reações de apoio em função de w, utilizando as equações de equilíbrio:
Passo 2
Com as reações calculadas, podemos esboçar, respectivamente, o diagrama de cortante e o de momento fletor:
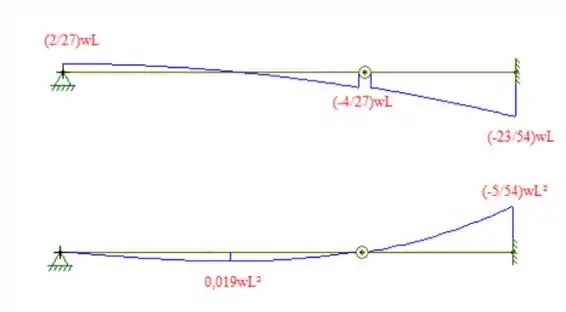
Resposta
Exercícios de Livros Relacionados
A viga suporta a carga distribuída mostrada. Determine as cargas internas resultallles que agem na seção transversal que passa pelo ponto C . Considere que as reações nos apoios A e B sejam verticais.
A estrutura do poste de energia elétrica suporta os três cabos, e cada um deles exerce uma força de 4k N nas escoras. Se as escoras estiverem acopladas por pinos em A , B e C , determine as cargas int
Determine as cargas internas resultantes que agem na seção transversal que passa pelo ponto B .
A carga de 4.000N está sendo levantada a uma velocidade constante pelo motor M, que pesa 450N . Determine as cargas internas resultantes que agem na seção transversal que passa pelo ponto B na viga. A
Determine a resultante das forças internas normal e de cisalhamento no elemento na seção b - b , cada uma em função de θ . Represente esses resultados em gráficos para 0 ≤ θ ≤ 90 ° . A carga de 650N é