Enunciado
Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 5.Problemas - Ex. 7
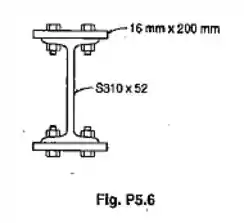
Resolva o Prob. 5.6, considerando que duas placas de 12 x 200 mm são usada para reforçar a viga mostrada.
Passo 1
Nessa questão são adicionadas duas barras a mais para reforçar as que já existiam no exercício anterior. Antes tinha-mos barras de 16 mm x 200 mm e agora foram adicionadas duas com 12 x 200 mm. Então, pararesolver esse exercício, vamos fingor que estamos simplesmente trabalhando com duas barras, mas as mesmas agora com 28 x 200 mm já que quando são sobrepostas é isso que acontece.
(essa foi minha interpretação do enunciado. Caso você entenda que o enunciado pede pra substituir a barra de 16 mm por uma de 12, é só você fazer o mesmo passo a passo que vou desenvolver, no entando admitindo duas barras de 12 x 200 mm).
Temos então do eunciado
Olhando na tabela para esse perfil temos
O será dado por
Passo 2
Temos ainda para Q
A fórmula que nos dá a tensão de cisalhamento é
No entando nós queremos determinar essa força
Como são dois parafusos:
Por ultimo ainda precisamos to momento de inércia total para aplicarmos a relação
Onde teremos para o momento de inércia
Onde 1 representa o perfil do meio e 2 e 3 as barras superiores e inferiores, que tem o mesmo momento de inércia.
Passo 3
Podemos então finalmente aplicar
Isolando então o V já que queremos o cisalhamento vertical
Prontinho