Enunciado
Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 10.Problemas - Ex. 31
Resolva o Problema 10.30 considerando que a força P é movida para C e atua verticalmente para baixo.
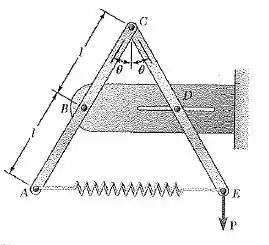
Passo 1
Para resolver este problema indico resolver o problema 10.29 e o problema 10.30, que pode ser visualizado no site.
A partir da análise feita dos problemas anteriores, e sabendo que a força P da figura do enunciado foi movida para o ponto C e está atuando verticalmente para baixo.
Passo 2
Achou um pouco complicado? Vamos destrinchar!
Observe na figura o triângulo , o ângulo é entre a hipotenusa BC e o cateto B’C. Desse modo:
Assumindo que, e que , temos:
Derivando:
Agora observe o triângulo , obtemos que:
Assumindo que, , temos:
Derivando,
Passo 3
Já estamos quase terminando! Vamos lembrar que a força na mola é dada por:
Onde s é o alongamento da mola, logo:
Portanto,
Passo 4
Pronto! Já temos a relação da força F, então basta utilizarmos o trabalho virtual que encontraremos a equação desejada.
Sabemos que, o trabalho virtual é 0. Ou seja,
E como,
Temos:
Logo,
Isolando, teremos:
Portanto
Passo 5
Substituindo os valores, temos que:
Resolvendo teremos:
Ou