Enunciado
Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 13.Problemas - Ex. 97
Resolva o problema 13.8, considerando que a corda elástica é substituída por uma força central F de intensidade voltada para .
Passo 1
Oooi, galerinha!
Essa questão deve ser feita com base no Problema Resolvido 13.8, sendo que a corda elástica que prende a esfera à origem deve ser substituída por voltada para . Observe a figura:
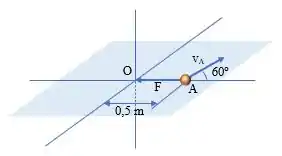
O enunciado fornece os seguintes dados:
E informa que a esfera pode deslizar sem atrito sobre a superfície horizontal. Na figura, vemos que
Nosso dever é determinar as distâncias máxima e mínima da esfera em relação a e as velocidades correspondentes.
Sabemos que a força exercida na esfera passa pela origem O e que o seu trabalho pode ser expresso como uma variação de energia potencial. Assim, a energia total da esfera e a quantidade de movimento angular em relação a são conservadas. Veja a figura:
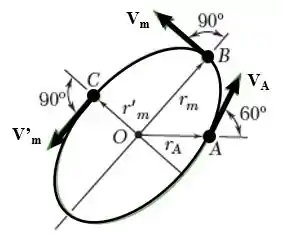
A distância da origem é máxima no ponto B, onde a velocidade da esfera é perpendicular ao segmento OB, e mínima no ponto C, onde a velocidade da esfera é perpendicular ao segmento OC.
Passo 2
Aplicando o princípio da conservação do momento angular em torno de O:
Passo 3
Calculando a energia cinética e potencial:
No ponto :
Sabendo que , e que
Temos que,
E sendo ,
Nos pontos e :
Passo 4
Aplicando agora o princípio da conservação de energia:
Substituindo pela expressão encontrada anteriormente:
Chegamos então a uma equação do 2º grau.
Passo 5
Resolvendo a equação encontramos os dois valores para , o máximo e o mínimo. Usaremos a fórmula de Bhaskara.
A distância máxima da esfera em relação a é
E a distância mínima é
Passo 6
Em posse das distâncias máxima e mínima, podemos calcular as velocidades correspondentes. Temos que,
Então, sendo :
E sendo :