Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 13.Problemas - Ex. 74

Um pacote de 200 g é lançado para cima com uma velocidade v 0 por uma mola em A; ele se move em torno de uma estrutura sem atrito e é depositado em C. Para cada uma das estruturas mostradas nas figuras, determine (a) a menor velocidade v 0 para que o pacote atinja C, (b) a força correspondente exercida pelo pacote sobre a estrutura justamente antes do pacote deixar a estrutura em C.

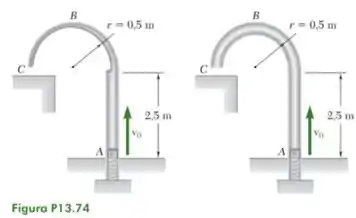
Fonte: Beer – Dinâmica – 9ª ed

Passo 1

Fala aí, tudo bem?

Bora pra mais uma?!

Bem, vamos analisar o problema de utilizando nossa amiga conservação de energia.

Façamos nossas considerações:

  1. Vamos comparar os dois instantes: Em A e em B. Assim, pois é mais fácil encontrar a velocidade em B, justamente porque nesse ponto não há força normal, e a resultante das forças é somente a força peso.

Veremos agora:

Como em B, o pacote está em movimento circular, o somatório das forças será a Força Centrípeta:

∑ F y = m v B 2 r       →   m v B 2 r = m g

Substituindo os valores:

  0,2 * v B 2 0,5 = 0,2 * 9,81             → v B = 2,21 m s

Passo 2

Descoberta a velocidade em B, podemos aplicar a conservação da energia entre os pontos, assim temos:

E M A = E M B     →     1 2 m v A 2 = 1 2 m v B 2 + m g h

Substituindo os valores:

  1 2 0,2 * v A 2 = 1 2 0,2 * 2,21 2 + 0,2 * 9,81 * ( 2,5 + 0,5 )

Assim:

v A = 7,99 m s

Passo 3

Podemos descobrir a velocidade em C também pela conservação da energia, entre os instantes A e C:

E M A = E M C     →     1 2 m v A 2 = 1 2 m v C 2 + m g h

Substituindo os valores:

  1 2 0,2 * 7,99 ² = 1 2 0,2 * v C 2 + 0,2 * 9,81 * ( 2 , 5 )

Assim:

v C = 3,84 m s

Antes do pacote deixar a barra e bater no ponto C, percebe-se que a única força atuante na horizontal no pacote é a Força Normal. Sabendo que a resultante é m v 2 r , podemos encontrar a força normal nesse instante:

N = 0,2 * 3,84 ² 0,5                 → N = 5,89   N

Passo 4

No segundo caso (tubo), podemos perceber que em B, a velocidade nesse instante pode ser nula, uma vez que o peso do pacote pode ser sustentado pelo próprio tubo, assim:

E M A = E M B     →     1 2 m v A 2 = m g h

Substituindo valores:

1 2 * 0,2 * v A 2 = 0,2 * 9,81 * 2,5 + 0,5               → v A = 7,67 m s

Passo 5

Podemos descobrir a velocidade em C também pela conservação da energia, entre os instantes A e C:

E M A = E M C     →     1 2 m v A 2 = 1 2 m v C 2 + m g h

Substituindo os valores:

  1 2 0,2 * 7 , 67 ² = 1 2 0,2 * v C 2 + 0,2 * 9,81 * ( 2,5 )

Assim:

v C = 3 , 13 m s

Antes do pacote deixar a barra e bater no ponto C, percebe-se que a única força atuante na horizontal no pacote é a Força Normal. Sabendo que a resultante é m v 2 r , podemos encontrar a força normal nesse instante:

N = 0,2 * 3 , 13 ² 0,5                 → N = 3,92   N

Resposta

Portanto:

Letra a)

Letra b)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Para o movimento descrito no Problema 13.96, determinar (a) a máxima distância entre a origem e o colar, (b) a velocidade correspondente. Dica: Resolva por tentativa e erro a equação obtida para r .)
Resolva o problema 13.8, considerando que a corda elástica é substituída por uma força central F de intensidade ( 80 / r 2 )N voltada para O .
Após completar sua missão de exploração na Lua, os dois astronautas da tripulação de um módulo de excursão lunar Apollo iriam preparar o retorno ao módulo de comando que orbitava na Lua a uma altitude
Um colar A de 5k g está preso a uma mola de constante 800N / m e comprimento indeformado de 450m m . O sistema é posto em movimento com r = 300m m , v θ = 5m / s e v r = 0 . Desprezando a massa da bar
Um colar A de 1,8 kg e um colar B de 0,7 kg podem deslizar sem atrito sobre uma estrutura que consiste da barra horizontal OE e da barra vertical CD, livre para girar em torno de CD. Os dois colares e