Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 17.Problemas - Ex. 105

Resolva o Problema 17.104, admitindo que o impacto entre A e D seja perfeitamente elástico.

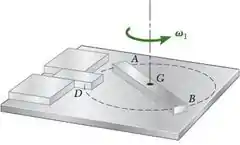
PROBLEMA 104 Uma barra delgada uniforme de comprimento L e massa m é apoiada por uma mesa horizontal sem atrito. Inicialmente, a barra está girando em torno de seu centro de massa G com uma velocidade angular constante ω 1 . Subitamente, o trinco D é movimentado para a direita, batendo na extremidade A da barra. Admitindo que o impacto entre A e D seja perfeitamente plástico, determine a velocidade angular da barra e a velocidade de seu centro de massa imediatamente após o impacto.

Passo 1

O exercício pede que a gente , determine a velocidade angular da barra e a velocidade de seu centro de massa imediatamente após o impacto

Momento de inércia é dada por:

I _ = 1 12 m L 2

Passo 2

Antes do impacto.

v A 1 = L 2 ω 1 ↓

Condição de impacto.

v A 2 = - e v A 1 = 1 2 e L ω 1 ↑

Cinemática depois do impacto.

v _ 2 = v A 2 + L 2 ω 2 = 1 2 e L ω 1 + 1 2 L ω 2

Passo 3

Princípio do impulso-momento no impacto.

Momentos sobre D:

I ω 1 + 0 = I ω 2 + m v _ 2 L 2

I ω 1 = I ω 2 + m 1 2 e L ω 1 + 1 2 L ω 2 L 2

1 12 m L 2 ω 1 = 1 12 m L 2 ω 2 + 1 4 m L 2 e ω 1 + 1 4 m L 2 ω 2

ω 2 = 1 4 1 - 3 e ω 1

v _ 2 = 1 2 L e ω 1 + 1 2 L 1 4 1 - 3 e ω 1 = 1 8 1 + e ω 1 L

Passo 4

Para um impacto perfeitamente plástico,

e = 1

ω 2 = 1 4 1 - 3 ω 1 = - 1 2 ω 1

v _ 2 = 1 2 L ω 1 + 1 2 L - 1 2 ω 1 = 1 4 L ω 1

Resposta

ω 2 = 1 2 ω 1  

v 2 = 1 4 L ω 1 ↑

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um pequeno reboque e sua carga têm uma massa total de 250 kg.O reboque é suportado por duas molas, cada uma de constante10 kN/m, e puxado sobre uma estrada cuja superfície pode ser aproximada por uma
Desenhe o análogo elétrico do sistema mecânico mostrado. (Dica: desenhe os loops correspondentes aos corpos livres m e A.)
Expresse em termos de L, C e E a faixa de valores da resistência R para a qual as oscilações ocorrerão no circuito mostrado quando a chave S for fechada.
Um elemento de máquina de 500 kg é suportado por duas molas, cada uma de constante 50 kN/m. Uma força periódica de 150 N de amplitude é aplicada ao elemento com uma frequência de 2,8 Hz. Sabendo que o
Escreva as equações diferenciais definindo (a) os deslocamentos da massa me do Ponto A, (b) as cargas nos capacitores do análogo elétrico.