Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 17.Problemas - Ex. 112

Uma barra delgada AB de comprimento L está em livre com uma velocidade v0 quando a corda AC se torna subitamente esticada. Considerando que o impacto é perfeitamente plástico, determine a velocidade angular da barra e a velocidade de seu centro de massa imediatamente depois da corda ficar esticada.

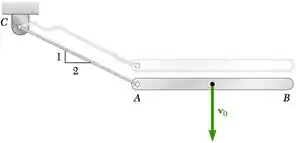
Passo 1

O exercício pede que a gente determine a velocidade angular da barra e a velocidade de seu centro de massa imediatamente depois da corda ficar esticada

Imediatamente após o impacto

tan ⁡ θ = 1 2                 θ = 26.565 °

Passo 2

Devido à restrição do cabo inextensível,

v A = v A     θ

Cinemática:

v G = v A + v G / A = v A     θ + L 2 ω ↓

Passo 3

Princípio de impulso e momentum.

Componentes θ :

m v 0 cos ⁡ θ + 0 = m v A + m L 2 ω cos ⁡ θ

v A + 1 2 cos ⁡ θ L ω = v 0 cos ⁡ θ

+ Momentos sobre A:

m v 0 L 2 + 0 = m v A cos ⁡ θ L 2 + m L 2 ω L 2 + I - ω

L 2 cos ⁡ θ v A + 1 4 L 2 + 1 12 L 2 ω = L 2 v 0

Passo 4

Resolvendo as Eqs. (2) e (3) simultaneamente (com θ = 26,565 ° )

v A = 0.55902 v 0                 L ω = 0.75 v 0

Velocidade do centro de massa.

v G = v A + v G / A

v G = 0.55902 v 0     θ + 1 2 0.75 v 0 ↓ = 0.25 v 0 ← + 0.5 v 0 ↓ + 0.375 v 0 ↓ = 0.25 v 0 ← + 0.875 v 0 ↓

Resposta

Velocidade angular depois do impacto

ω = 0.750 v 0 L

v B = 0.910 v 0     74.1 °

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

19.113. Um motor de massa M é suportado por molas com uma constante de mola equivalente k. O desbalanceamento de seu rotor é equivalente a uma massa m localizada a uma distância r do eixo de rotação.
19.118. Um motor de 180 kg é parafusado a uma viga horizontal leve. O desbalanceamento do seu rotor é equivalente a uma massa de 28 g localizada a 150 mm do eixo de rotação e a deflexão estática da vi
19.120. Um medidor de vibração, usado para medir a amplitude das vibrações, consiste de uma caixa contendo um sistema massa-mola com frequência natural conhecida de 120 Hz. A caixa está rigidamente li
19.119. O desbalanceamento do rotor de um motor de 200 kg é equivalente a uma massa de 100 g localizada a 150 mm do eixo de rotação. A fim de limitar para 1 N a intensidade da força oscilante exercida
19.119. Um motor de 180 kg é suportado por molas de constante total 150 kN/m. O desbalanceamento do rotor é equivalente a uma massa de 28 g localizado a 150 mm do eixo de rotação. Determine o interval