Enunciado
Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 18.Problemas - Ex. 13
Resolva o Problema 18.12, se o coeficiente de atrito cinético entre a bobina e o plano em A for .
Passo 1
Começaremos o exercício analisando o diagrama a seguir para o sistema:
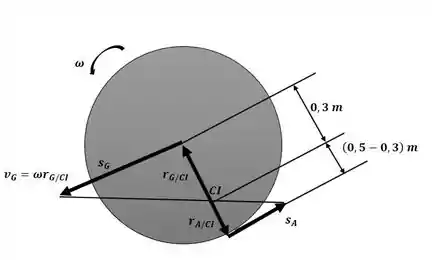
Sendo assim, conseguimos escrever uma relação entre e por semelhança de triângulos:
Passo 2
Agora podemos analisar o diagrama de corpo livre do sistema e aplicar o somatório de forças na direção normal:
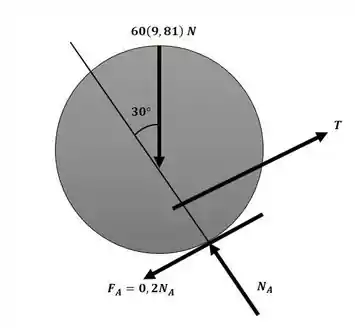
Passo 3
Agora aplicaremos o princípio do trabalho e energia para o sistema, com base nos diagramas apresentados nos passos 1 e 2:
Substituindo a relação encontrada no passo 1:
Resposta
Exercícios de Livros Relacionados
3/127)Um pequeno veículo de teste com um foguete de propulsão com uma massa total de 100k g parte do repouso em A e se desloca com atrito desprEzível ao longo da pista no plano vertical como mostrado
3/137) É determinado experimentalmnte que as rodas motrizes de um carro devem exercer uma força de tração de 560N sobre a superfície da estrada a fim de manter uma velocidade constante do veículo de 9
3/132) A esfera é liberada a partir da posição A com uma velocidade de 3m / s e oscila em uma plano vertical . Na posição maisi baixa , o cordão bate na barra fixa em B , e a esfera continua a oscilar
3/123) Aunidade motora A é utilizada para elevar o cilindro de 300k g a uma taxa constante de 2m / s . Se o medidor de potência B registra uma entrada de potência elétrica de 2,20k W , calcule a efici
3/134) O sistema é liberado a partir do repouso na posição mostrada . O cilindro de 15k g cai através do orifício no suporte , mas o disco de 15k g ( mostrado em corte) é removido do cilindro quando e