Enunciado
Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 18.Problemas - Ex. 29
Quando uma força P = 150 N é aplicada à alavanca do freio, o cilindro A, de 25 kg, está descendo a uma velocidade de 6 m/s. Determine o número de revoluções que a roda B rotacionará antes que seja parada. O coeficiente de atrito cinético entre a sapata do freio C e a roda é . A massa da roda é 12,5 kg, e o raio de giração em relação a seu centro de massa é .
Passo 1
Começaremos o exercício encontrando o valor da reação normal em C através do somatório de momento com relação ao ponto D com o auxílio da figura a seguir:
Como a roda gira em torno de um eixo fixo, a velocidade angular da roda pode ser dada por:
O momento de inércia da roda com relação ao seu centro de massa é dada por:
Sendo assim, a energia cinética do sistema na sua posição inicial é dada por:
Passo 2
Como o sistema é levado ao repouso, , com base a no diagrama a seguir:
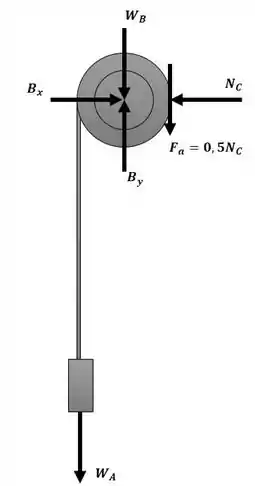
Sabemos que e não realizam trabalho, equanto e realizam. Quando a roda B rotaciona de um ângulo , se desloca de:
E ainda, o ponto C se desloca de:
Sendo assim, o trabalho realizado por e é dado por:
Passo 3
Agora iremos aplicar o princípio do trabalho e da energia: