Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 3.6 - Ex. 127
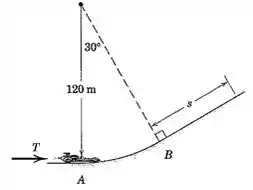
3/127)Um pequeno veículo de teste com um foguete de propulsão com uma massa total de parte do repouso em e se desloca com atrito desprEzível ao longo da pista no plano vertical como mostrado , Se o foguete propulsor exerce um empuxo constante de a partir de até a posição onde este é desligado , determine a distância que o veículo percorre para cima na inclinação antes de parar . A perda de massa devido à espulsão de gases pelo foguete é pequena e pode ser desprezada .
Passo 1
Então pessoal , a primeira coisa que devemos fazer é encontrar o comprimento . E para isso devemos lembrar de como calculamos o comprimento de arcos . Temos que :
Em que está em radianos . Sendo assim , devemos passar para radianos através da fórmula :
Logo , para :
Passo 2
Para acharmos a elevação vertical que o veículo apresenta ao sair do ponto para o ponto , fazendo a análise na figura do enunciado , faremos uso da trigonometria básica através da equação :
Usando a equação de trabalho-energia que afirma que o trabalho total realizado por todas as forças é igual a variação na energia cinética da partícula , achamos que :
Uma vez que :
Sendo assim ,
Isolando na equação , obtemos que :
Resposta
E aí , topa fazer mais exercícios com a gente?