Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 9.Problemas - Ex. 8

8. Resolva o Problema 9.4 usando as equações de transformação de tensão desenvolvidas na Seção 9.2.

Passo 1

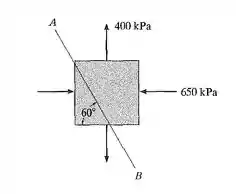
Olhando a figura do enunciado, tiramos do estado plano de tensão, que:

σ x = - 650   k P a , tensão normal de compressão no eixo x

σ y = 400   k P a , tensão normal de tração no eixo y

τ x y = 0 , não há tensão cisalhante de acordo com nossa figura

φ = 60 ° , é o ângulo do plano inclinado com a horizontal

θ = 30 ° , é o ângulo que o plano inclinado forma com a vertical, considerando que os nossos eixos estão rotacionados no sentido anti-horário positivo. É esse ângulo, que utilizaremos em nossos cálculos.

Passo 2

O que temos que fazer agora, é aplicar as equações de transformação de tensão para determinar o valor de σ x ' , σ y ' e τ x ' y '

Sabemos que σ x ' é dado em função das tensões normais σ x e σ y e da tensão cisalhante τ x y , pela seguinte fórmula:

σ x ' = σ x + σ y 2 + σ x - σ y 2 cos ⁡ 2 θ + τ x y sen ⁡ 2 θ

Substituímos os valores numéricos pertinentes a cada variável:

σ x ' = ( - 650   k P a + 400   k P a ) 2 + ( - 650   k P a - 400   k P a ) 2 cos ⁡ ( 60 ° )

σ x ' = - 387,5   k P a

σ x ' ≈ - 0,387   M P a

E sabemos também, que σ y ' tem a seguinte cara:

σ y ' = σ x + σ y 2 - σ x - σ y 2 cos ⁡ 2 θ ⁡ -   τ x y sen ⁡ 2 θ

Substituímos os valores numéricos de cada variável:

σ y ' =   ( - 650   k P a + 400 k P a ) 2 - ( - 650   k P a - 400   k P a ) 2 cos ⁡ 60 °

σ y ' = 137,5   k P a

σ y ' ≈ 0,137   M P a

Por fim, vamos usar a fórmula da transformação de tensão para encontrar a tensão cisalhante τ x ' y ' , que tem a seguinte aparência:

τ x ' y ' = - σ x - σ y 2 sen ⁡ 2 θ ⁡ +   τ x y cos ⁡ 2 θ

Substitui-se os valores numéricos adequados e chega-se a:

τ x ' y ' = - σ x - σ y 2 sen ⁡ 2 θ ⁡ +   τ x y cos ⁡ 2 θ

τ x ' y ' = - ( - 650   k P a - 400   k P a ) 2 sen ⁡ 60 °

τ x ' y ' = 454,66   k P a

τ x ' y ' ≈ 0,455   M P a

Pronto! Encontramos nossas respostas!

Resposta

σ x ' ≈ - 0,387   M P a

σ y ' ≈ 0,137   M P a

τ x ' y ' ≈ 0,455   M P a

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

25. Um bloco de madeira falhará, se a tensão de cisalhamento que age ao longo da fibra for 3,85M P a . Se a tensão normal σ x = 2,8M P a , determine a tensão de compressão σ y necessária para provocar
2. O estado de tensão em um ponto em um elemento estrutural é mostrado no elemento. Determine as componentes de tensão que agem no plano inclinado A B . Resolva o problema usando o método do equilíbri
O estado de tensão em um ponto em um elemento estrutural é mostrado no elemento. Determine as componentes de tensão que agem no plano inclinado A B . Resolva o problema usando o método do equilíbrio d
3. O estado de tensão em um ponto em um elemento estrutural é mostrado no elemento. Determine as componentes de tensão que agem no plano inclinado A B . Resolva o problema usando o método do equilíbri
6. O estado de tensão em um ponto em um elemento estrutural é mostrado no elemento. Determine as componentes de tensão que agem no plano inclinado A B . Resolva o problema usando o método do equilíbri