Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 9.Problemas - Ex. 6
6. O estado de tensão em um ponto em um elemento estrutural é mostrado no elemento. Determine as componentes de tensão que agem no plano inclinado . Resolva o problema usando o método do equilíbrio descrito na Seção .
Passo 1
Primeiro, vamos montar o esquema do elemento seccionado pela reta A-B:
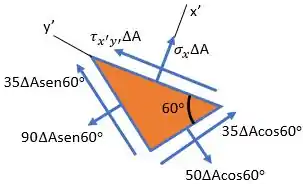
Passo 2
Agora, faremos a somatória de forças em e igualaremos a zero para acharmos a tensão , lembrando que :
Passo 3
Então, em seguida, faremos a somatória das forças em como no passo anterior e igualaremos a zero para achar a tensão , lembrando que :
O valor negativo que foi encontrado, indica que a tensão ocorre no sentido oposto ao apresentado no esquema do corte
Resposta
A tensão normal que age plano é:
E a tensão de cisalhamento é:
Exercícios de Livros Relacionados
7. Resolva o Problema 9.2 usando as equações de transformação de tensão desenvolvidas na Seção 9.2.
8. Resolva o Problema 9.4 usando as equações de transformação de tensão desenvolvidas na Seção 9.2.
9. Resolva o Problema 9.6 usando as equações de transformação de tensão desenvolvidas na Seção 9.2. Moste o resultado em um desenho.
11. Determine o estado de tensão equivalente em um elemento, se ele estiver orientado a 60 ° em sentido horário em relação ao elemento mostrado
10. Determine o estado de tensão equivalente em um elemento se ele estiver orientado a 30° em sentido anti-horário em relação ao elemento mostrado. Use as equações de transformação de tensão.