Uma informação que ele nós dá é que uma barra de diâmetro só pode suportar uma carga máxima de . Com isso podemos determinar a tensão máxima adimissivel na estrutura que será dada por:

Se temos a tensão admissível, conseguimos relacionar ela com o fator de segurança dado por:

Como já sabemos o , só falta definirmos o valor do normal na barra AB. Sneod assim termeos que:

• Seção de Richter para a barra AB





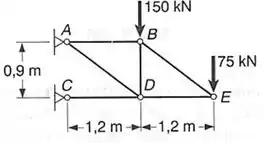
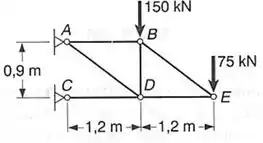
Perceba que se fizermos o somatório de momentos em torno do ponto D, sumiremos com os normais da barra BD e DE, e ainda sumimos coma carga de 150, sendo assim teremos que:

Para definir o fator de segurança basta a gente fazer:

E assim resolvemos a questão A.

Passo 2

Se queremos definir um diâmetro a partir de um fator de segurança podemos fazer o seguinte.

Já sabemos pelo enunciado que: .

Sabemos também que a fórmula que nós da a tensão aplicada é dada por:

A força aplicada vamos descobrir daqui a pouco resolvendo a nossa treliça. A área aplicada vai ser exatamente o que vai os ajudar a descobrir o diâmetro da nossa barra, sendo assim podemos escrever que:

Substituindo na nossa fórmula de fator de segurança teremos que:

E como o nosso objetivo é determinar o diâmetro teremos que:

Sabemos que:

Perceba que comos estamos usando a tensão admissível em , significa que a nossa força aplicada tem que ser em e o diâmetro vai sair em , sendo assim substituindo os valores teremos que:

• Equilíbrio do nó E





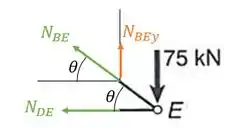
Decompondo os vettores teremos que:

Perceba que para determinar o seno do ângulo, precisamos das barras BD e BE, e com isso teremos que:

Fazendo o equilíbrio teremos que:

Passo 3

Agora é tranquilo, se o nosso objetivo é determinar o diâmetro das nossas barras, basta usarmos a nossa formulazinha:

• BE