Enunciado
Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 2.Problemas - Ex. 30
Uma carga vertical P é aplicada no centro A da face superior de um tronco de cone circular de altura h e com raio mínimo igual a e raio máximo igual a b. Denotando por E o modulo de elasticidade do material e desprezando o efeito do peso próprio, determine a deflexão do ponto A.
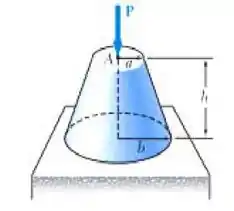
Passo 1
Fala ai gurizada tudo belezinha? Para determinarmos a deflexão vamos primeiramente realizar um esboço do diagrama de corpo livre, estendendo o lado inclinado do cone e determinando a origem, vejam....
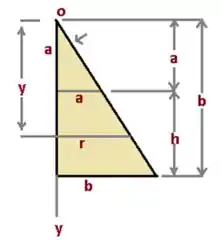
Da geometria exposta consideramos que:
Então temos....
Passo 2
Na coordenada do topo temos que a área é:
E a deformação em
E a deformação total:
Resposta
Exercícios de Livros Relacionados
O estado plano de tensões mostrado ocorre em uma barra feita de uma classe de aço, cuja tensão de escoamento à tração é de 310M P a . Determinar o coeficiente de segurança, em relação ao escoamento, u
Uma barra de alumínio fundido é feito de uma liga em que σ U T = 80M P a e σ U C = 200M P a . Sabendo-se que a intensidade T dos torques aplicados é gradual e crescente e usando o critério de Mohr, de
O vaso de pressão cilíndrico mostrado é fabricado com chapas de aço de 6,35 m m de espessura, soldada ao longo de uma hélice, formando um ângulo de 30 ° com a horizontal. Sabendo-se que a tensão norma
Para o estado de tensões mostrado, determinar a máxima tensão de cisalhamento, quando: σ y = + 80M P a σ y = - 80M P a
Nós expressamos por ε 1 , ε 2 e ε 3 as três medidas de deformação específica normal feitas com uma roseta à 60°. Pede-se (b) Sabendo-se que as seguintes medidas foram feitas com esta roseta, em um dad