Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 2.Problemas - Ex. 40

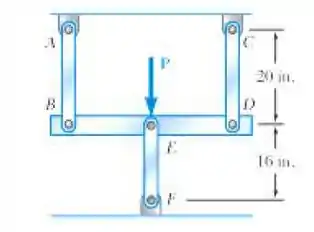
Três barras de aço ( E = 29   x   10 6   p s i ) suportam uma carga P de 8,5 - k i p . Cada uma das barras AB e CD tem uma área de seção transversal de 0,32 - i n ² , e a barra EF tem uma área de seção transversal de 1 - i n ² . Desprezando a deformação da barra BED, determine (a) a variação do comprimento da barra EF e (b) a tensão em cada barra.

Passo 1

Fala aí galera tudo belezinha???? Antes de mais nada vamos desenhar nosso famoso e querido diagrama de corpo livre para facilitar os cálculos, vejam...

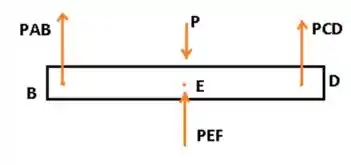
Por simetria, ou por ∑ M E = 0 temos que:

P C D = P A B

Realizando o somatório das forças em Y temos: + ↑ ∑ F y = 0 :       P A B + P C D + P E F - P = O P = 2 P A B +   P E F  

Sendo que o alongamento é dado pela equação abaixo... δ A B = P A B L A B E A A B           δ C D = P C D L C D E A C D       δ E F = P E F L E F E A E F  

Consideramos que :

L A B = L C D     e     A A B = A C D ,     δ A B = δ C D

Como os pontos A, C, e F foram fixos, temos que seus alongamentos são:

δ B = δ A B ,     δ D = δ C D ,     δ E = δ E F

Como o elemento BED é rígido

δ E = δ B = δ C

Passo 2

Então gurizada depois que a gente definiu os alongamentos vamos determinar como encontrar a força P:

P A B L A B E A A B = P E F L E F E A E F         ∴       P A B = A A B A E F   x   L E F L A B x   P E F = 0,32 1   x   16 20   x   P E F = 0,256 P E F

Lembrando do somatório das forcas que realizamos no passo 1 temos que:

P = 2 P A B + P E F = 2   x   0,256 P E F +   P E F = 1,512 P E F

P E F = P 1,512 = 8,5 1,512 = 5,6217   k i p s  

      P A B = P C D = 0,256   x   5,6217 = 1,43916   k i p s  

Agora podemos calcular o alongamento e a tensão apenas aplicando na equação e prontinho :D

  1. δ E F = P E F L E F E A E F =   5,6217   x   ( 16 ) 29   x   10 3   x   ( 1 ) = 0,0031016   i n .

  2. σ A B = σ C D =   P A B A A B = 1,43916 0,32 = 4,4974   k s i σ E F = P E F A E F = 5,6217 1 = 5,6217   k s i

Resposta

  1. δ E F = 0,00310 i n .

  2. σ A B = σ C D = 4,50   k s i σ E F = 5,62   k s i
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um bloco de 10 in. de comprimento e seção transversal de 1,8x1,6i n deve suportar uma força de compressão centrada P. O material a ser utilizado é um bronze para o qual E = 14x10 6 p s i . Determine a
Duas marcas de referência são colocadas a exatamente 250 mm uma da outra, em uma barra de alumínio haste com E=73G P a e resistência última de 140 MPa com diâmetro de 12 mm. Sabendo que a distancia en
O sólido mostrado foi cortado de uma chapa de vinil com 1 4 in de espessura (E = 0,45x10 6 p s i ) e é submetido a uma tração de 350 lb. Determine (a) a deformação total do sólido, (b) a deformação de
Um cabo de aço de 4,8 ft de comprimento de ¼ in de diâmetro é submetido a uma ação de tração de 750 lb. Sabendo que E=29X10 6 p s i . Determine (a) o alongamento do arame, (b) a correspondente tensão
Uma haste de controle de aço com 5,5 ft de comprimento não pode sofrer estiramento maior que 0,04 in, quando uma ação de tração de 2 kip lhe é aplicada. Sabendo que E = 29x10 6 psi, determine (a) o me