Enunciado
Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 2.Problemas - Ex. 39
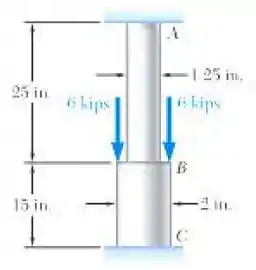
uma haste de poliestireno consiste em duas partes cilíndricas AB e BC engastadas em ambas as extremidades e suportando duas ações de 6 kip conforme mostrado. Sabendo que . Determine (a) as reações em A e C, (b) a tensão normal em cada parte da haste.
Passo 1
Fala aí pessoal tudo belezinha???? Partiu determinarmos as reações vamos desenhar um digrama de corpo livre para facilitar os cálculos, vejam :D
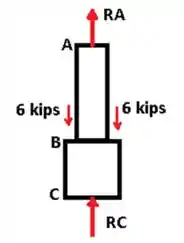
Expressamos que o alongamento da haste zero seja:
(1)
Então vamos considerar que:
(2)
Substituindo 2 em 1 e simplificando temos:
Passo 2
Observem que no diagrama do corpo livre temos:
(1)
Sabendo que :
(2)
Substituição (1) por (2)
Apartir de (1) temos:
Passo 3
Agora bastaa aplicarmos na equação para encontrarmos as tensões, barbadinha :D
Resposta
Exercícios de Livros Relacionados
Um anel de latão de 130 m m de diâmetro externo e espessura de 6 m m se encaixa perfeitamente dentro de um outro aço de 130 m m de diâmetro interno e espessura de 3 m m , quando a temperatura de ambos
O tanque de ar comprimido AB tem um diâmetro externo de 462 m m e uma espessura uniforme e 6 m m . Sabendo-se que a pressão dentro do vaso é de 130k P a , determinar a máxima tensão normal e a máxima
Um cabo de aço de 18 m de comprimento e 5 mm de diâmetro será usado na fabricação de uma viga de concreto protendido. Observa-se que o cabo sofre um estiramento de 45 mm quando a força P é aplicada. S
Uma haste de aço com 4 m de comprimento não pode ser estirada em mais de 3 mm, e a tensão normal não deve exceder 150 MPa quando a haste é submetida a uma força axial de 10 kN. Sabendo que E = 200G P
Um tubo de alumínio não deve sofrer um estiramento maior que 0,05 in quando submetido a tensão de tração. Sabendo que E = 10,1x10 6 psi e que a tensão normal máxima admissível é de 14 ksi, determine (