Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 2.Problemas - Ex. 37

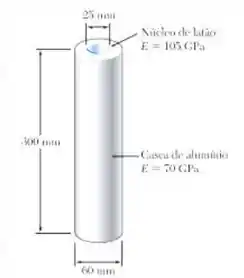
Uma força axial de 200 kN é aplicada através de placas rígidas colocadas nas extremidades da montagem mostrada. Determine (a) a tensão normal na casca de alumínio, (b) a correspondente deformação da montagem.

Passo 1

Fala aí galera tudo belezinha???? Partiu determinar a tensão do elemento de alumínio, vem comigo!! Vamos considerar o alongamento abaixo:

δ =   P a L E a A a ,       o u     P a =   E a A a L δ

δ =   P b L E b A b ,       o u     P b =   E b A b L δ

Onde:

P a = porção da força axial transportada pelo casco.

P b = porção da força axial transportada pelo núcleo.

Portanto, P =   P a +   P b = E a A a +   E b A b δ L (1)

Notem que é necessário que nós calculemos a área de ambas as porções, então vem comigo!!

A a = π 4 0,060 2 - 0,025 2 = 2,3366   x   10 - 3 m 2 (2) A b = π 4 0,025 2 = 0,49087   x   10 - 3 m 2 (3)

Substituindo 2 e 3 em 1 temos: P = 70   x   10 9   x   2,3366   x   10 - 3 +   105   x   10 9   x   0,49087   x   10 - 3 δ L P = 215,10   x   10 6 δ L

Passo 2

Agora gurizada que encontramos a força P temos que determinar a deformação, porque olhem a equação da tensão abaixo, não temos essa informação ☹

σ a = E a ε

Encontrando a deformação podemos determinar a tensão

ε = δ L = P 215 ,   10   x   10 6 = 200   x   10 3 215 ,   10   x   10 6 = 0,92980   x   10 - 3

Agora temos todas as informações necessárias para encontrar a tensão e o alongamento, basta que a gente aplique na equação :D

  1. σ a = E a ε = 70   x   10 9   x   0,92980   x   10 - 3 = 65,1   x   10 6 P a
  2. δ = ε L = 0,92980   x   10 - 3   x   ( 300 m m )

Resposta

  1. σ a = 65,1   M P a
  2. δ = 0,279   m m
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Nós expressamos por ε 1 , ε 2 e ε 3 as três medidas de deformação específica normal feitas com uma roseta à 60°. Pede-se (a) mostrar que a soma destas deformações e a soma do quadrado de suas diferenç
O círculo de Mohr mostrado corresponde ao estado de tensões dado nas Figs. 6.5a e b, Sec. 6.1. Notando que σ x ' = O C ' - C X ' cos ⁡ 2 θ p - 2 θ e que τ x ' y ' = C X ' s e n ( 2 θ p - 2 θ ) , desen
Sabendo-se que o diâmetro da barra de aço A B D é 30m m , determinar (a) os planos principais; (b) as tensões principais; (c) a máxima tensão de cisalhamento, no ponto H .
O tanque de ar comprimido AB tem um diâmetro externo de 462 m m e uma espessura uniforme e 6 m m . Sabendo-se que a pressão dentro do vaso é de 130k P a , determinar a máxima tensão normal e a máxima
Resolver o P r o b . 6.114 , considerando que o anel de latão é de 3 m m de espessura e o anel de aço de 6 m m de espessura.